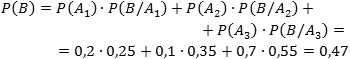Предположим, что событие B может произойти только с одним из несовместных событий A1, A2, ..., An. Например, на склад поступает оборудование от нескольких производителей, причем от каждого из них может поступить разное количество оборудования. Также может различаться и вероятность брака у каждого производителя.
Из совокупной партии оборудования случайным образом выбирается один образец. Как определить вероятность того, что этот образец окажется бракованным?
Пусть в совокупной партии встречается только оборудование производителей A1, A2, ..., An. Тогда вероятность события Bk (получить бракованный образец) для k-го производителя считается по формуле условной вероятности:
![]()
Важно понимать, что P(Ak) — это вероятность наткнуться на образец от k-го производителя во всей партии, P(B/Ak) — это вероятность брака именно в партии от k-го производителя. Поскольку оборудование не может принадлежать сразу двум производителям, события A1, A2, ..., An несовместны. По теореме сложения вероятностей получаем:
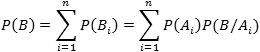
Это и есть формула полной вероятности. Она работает только если события A1, A2, ..., An покрывают все возможные исходы опыта, и позволяет найти вероятность нового события через его условные вероятности при условиях A1, A2, ..., An.
Вообще говоря, теория вероятностей сегодня активно изучается не только в университетах, но и в школах. Как следствие, этот вопрос относится не только к компетенции репетиторов по высшей математике в Москве, но и к обычным школьным учителям. Поэтому задача, которую мы рассмотрим далее, будет одинаково полезна и школьникам, и студентам.
Задача. На склад поступает оборудование от трех разных производителей. От первого поступило 20 образцов, от второго — 10, а от третьего — 70. Вероятность брака у этих производителей соответственно равна 0,25; 0,35 и 0,55. Найти вероятность получить бракованный образец при выборе наугад.
Всего у нас 20 + 10 + 70 = 100 образцов. Поэтому вероятность события A1, что образец получен именно от первого производителя (от него поступило 20 образцов), равна P(A1) = 20/100 = 0,2.
Аналогично, P(A2) = 10/100 = 0,1; P(A3) = 70/100 = 0,7. События A1, A2 и A3 попарно несовместны и в сумме покрывают пространство всех возможных событий. Применяем формулу полной вероятности: