Рассмотрим последовательность из $n$ независимых опытов, в каждом из которых событие $A$ может произойти с вероятностью $p$, либо не произойти — с вероятностью $q=1-p$. Обозначим через P n (k) вероятность того, что событие $A$ произойдет ровно $k$ раз из $n$ возможных.
В таком случае величину P n (k) можно найти по теореме Бернулли (см. урок «Схема Бернулли. Примеры решения задач»):
![]()
Эта теорема прекрасно работает, однако у нее есть недостаток. Если $n$ будет достаточно большим, то найти значение P n (k) становится нереально из-за огромного объема вычислений. В этом случае работает Локальная теорема Муавра — Лапласа, которая позволяют найти приближенное значение вероятности:
Локальная теорема Муавра — Лапласа. Если в схеме Бернулли число $n$ велико, а число $p$ отлично от 0 и 1, тогда:
Функция φ(x) называется функцией Гаусса. Ее значения давно вычислены и занесены в таблицу, которой можно пользоваться даже на контрольных работах и экзаменах.
Функция Гаусса обладает двумя свойствами, которые следует учитывать при работе с таблицей значений:
Локальная теорема Муавра — Лапласа дает отличное приближение формулы Бернулли, если число испытаний n достаточно велико. Разумеется, формулировка «число испытаний достаточно велико» весьма условна, и в разных источниках называются разные цифры. Например:
На мой взгляд, достаточно просто взглянуть на условие задачи. Если видно, что стандартная теорема Бернулли не работает из-за большого объема вычислений (например, никто не будет считать число 58! или 45!), смело применяйте Локальную теорему Муавра — Лапласа.
К тому же, чем ближе значения вероятностей $q$ и $p$ к 0,5, тем точнее формула. И, наоборот, при пограничных значениях (когда $p$ близко к 0 или 1) Локальная теорема Муавра — Лапласа дает большую погрешность, значительно отличаясь от настоящей теоремы Бернулли.
Однако будьте внимательны! Многие репетиторы по высшей математике сами ошибаются в подобных расчетах. Дело в том, что в функцию Гаусса подставляется довольно сложное число, содержащее арифметический квадратный корень и дробь. Это число обязательно надо найти еще до подстановки в функцию. Рассмотрим все на конкретных задачах:
Задача. Вероятность рождения мальчика равна 0,512. Найдите вероятность того, что среди 100 новорожденных будет ровно 51 мальчик.
Итак, всего испытаний по схеме Бернулли n = 100. Кроме того, p = 0,512, q = 1 − p = 0,488.
Поскольку n = 100 — это достаточно большое число, будем работать по Локальной теореме Муавра — Лапласа. Заметим, что n · p · q = 100 · 0,512 · 0,488 ≈ 25 > 20. Имеем:
![]()
Поскольку мы округляли значение n · p · q до целого числа, ответ тоже можно округлить: 0,07972 ≈ 0,08. Учитывать остальные цифры просто нет смысла.
Задача. Телефонная станция обслуживает 200 абонентов. Для каждого абонента вероятность того, что в течение одного часа он позвонит на станцию, равна 0,02. Найти вероятность того, что в течение часа позвонят ровно 5 абонентов.
По схеме Бернулли, n = 200, p = 0,02, q = 1 − p = 0,98. Заметим, что n = 200 — это неслабое число, поэтому используем Локальную теорему Муавра — Лапласа. Для начала найдем n · p · q = 200 · 0,02 · 0,98 ≈ 4. Конечно, 4 — это слишком мало, поэтому результаты будут неточными. Тем не менее, имеем:
![]()
Округлим ответ до второго знака после запятой: 0,17605 ≈ 0,18. Учитывать больше знаков все равно не имеет смысла, поскольку мы округляли n · p · q = 3,92 ≈ 4 (до точного квадрата).
Задача. Магазин получил 1000 бутылок водки. Вероятность того, что при перевозке бутылка разобьется, равна 0,003. Найти вероятность того, что магазин получит ровно две разбитых бутылки.
По схеме Бернулли имеем: n = 1000, p = 0,003, q = 0,997. Отсюда n · p · q = 2,991 ≈ 1,732 (подобрали ближайший точный квадрат). Поскольку число n = 1000 достаточно велико, подставляем все числа в формулу Локальной теоремы Муавра — Лапласа:
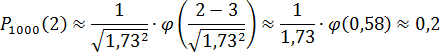
Мы сознательно оставляем лишь один знак после запятой (на самом деле там получится 0,1949...), поскольку изначально использовали довольно грубые оценки. В частности: 2,991 ≈ 1,732. Тройка в числителе внутри функции Гаусса возникла из выражения n · p = 1000 · 0,003 = 3.