Многие ученики ненавидят эту задачу и даже не пытаются ее решать. И совершенно зря, потому что смеси и сплавы — одни из самых легких задач B14.
Для решения требуется выполнить три простых шага:
Если все сделать правильно, то получится одно-два линейных уравнения. Решаем их — получаем ответ. А вот фиг! После того, как решите уравнение, никогда (слышите, никогда!) не записывайте ответ. Запомните:
Прежде чем записать ответ, вернитесь к задаче и еще раз прочитайте, что требуется найти. Потому что решить уравнение — это еще не значит решить текстовую задачу.
Это правило работает для всех текстовых задач, а не только для B14. Многие ученики сосредотачиваются на решении уравнения, но совершенно забывают, что, собственно, требовалось найти. Получается, что по существу задача решена верно, а ответ — неправильный.
Задача. Смешали 4 литра 15-процентного водного раствора некоторого вещества с 6 литрами 25-процентного водного раствора того же вещества. Сколько процентов составляет концентрация полученного раствора?
Итак, у нас есть три вещества:
Составим таблицу:
| Смесь | Общая масса, кг | Масса чистого вещества, кг |
| Раствор 1 (15%) | 4 | 0,15 · 4 = 0,6 |
| Раствор 2 (25%) | 6 | 0,25 · 6 = 1,5 |
| Раствор 3 | x | y |
По условию, нам не дана ни масса нового раствора, ни масса чистого вещества в нем. Поэтому обозначим общую массу x, а массу основного вещества y.
Поскольку при смешивании все массы складываются, получаем уравнения:
4 + 6 = x ⇒ x = 10;
0,6 + 1,5 = y ⇒ y = 2,1.
Уравнения получились настолько простыми, что даже не пришлось составлять систему. Но это еще не ответ! В задаче требуется найти концентрацию нового раствора. Чтобы найти ее, разделим массу чистого вещества на общую массу раствора:
y : x = 2,1 : 10 = 0,21
Итак, доля чистого вещества равна 0,21. Чтобы перевести долю в проценты, умножим на сто:
0,21 · 100 = 21
Задача. Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
Обозначим массу 30-процентного раствора x, а массу 60-процентного раствора y. Получим таблицу:
| Смесь | Общая масса, кг | Масса чистого вещества, кг |
| Раствор 1 (30%) | x | 0,3x |
| Раствор 2 (60%) | y | 0,6y |
| Чистая вода | 10 | 0 |
| Раствор 3 (50%) | 10 | 0,5 · 10 = 5 |
| Смесь «30% + 60% + вода» | x + y + 10 | 0,3x + 0,6y + 0 |
| Смесь «30% + 60% + 50%» | x + y + 10 | 0,3x + 0,6y + 5 |
По условию, концентрация смеси «30% + 60% + вода» равна 36%. Получаем уравнение:
0,3x + 0,6y + 0 = 0,36 · (x + y + 10)
Аналогично, концентрация смеси «30% + 60% + 50%» равна 41%. Отсюда получаем еще одно уравнение:
0,3x + 0,6y + 5 = 0,41 · (x + y + 10)
Решаем полученную систему, вычитая первое уравнение из второго:
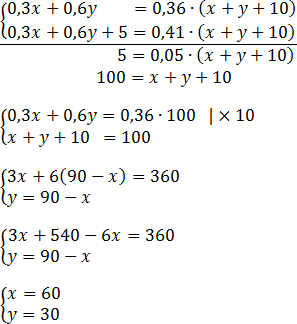
Теперь вспомним, что надо найти. А нужна масса 30-процентного раствора. Та самая, которую мы обозначили за x. Следовательно, x = 60 — это и есть ответ.
В заключение — два слова об уравнениях. Взгляните на задачи, приведенные выше: все уравнения — линейные. Никаких квадратов, никаких дискриминантов и тем более дробно-рациональных выражений. Вот почему задачи на смеси и сплавы считаются очень легкими.