Задачи B6 с монетами

Задачи на подбрасывание монет считаются довольно сложными. И перед тем как решать их, требуется небольшое пояснение. Задумайтесь, любая задача по теории вероятностей в итоге сводится к стандартной формуле:

Основная формула теории вероятностей

где p — искомая вероятность, k — число устраивающих нас событий, n — общее число возможных событий.

Большинство задач B6 решаются по этой формуле буквально в одну строчку — достаточно прочитать условие. Но в случае с подбрасыванием монет эта формула бесполезна, поскольку из текста таких задач вообще не понятно, чему равны числа k и n. В этом и состоит вся сложность.

Тем не менее, существует как минимум два принципиально различных метода решения:

  1. Метод перебора комбинаций — стандартный алгоритм. Выписываются все комбинации орлов и решек, после чего выбираются нужные;
  2. Специальная формула вероятности — стандартное определение вероятности, специально переписанное так, чтобы было удобно работать с монетами.

Для решения задачи B6 надо знать оба метода. К сожалению, в школах изучают только первый. Не будем повторять школьных ошибок. Итак, поехали!

Метод перебора комбинаций

Этот метод еще называется «решение напролом». Состоит из трех шагов:

  1. Выписываем все возможные комбинации орлов и решек. Например: ОР, РО, ОО, РР. Число таких комбинаций — это n;
  2. Среди полученных комбинаций отмечаем те, которые требуются по условию задачи. Считаем отмеченные комбинации — получаем число k;
  3. Осталось найти вероятность: p = k : n.

К сожалению, этот способ работает лишь для малого количества бросков. Потому что с каждым новым броском число комбинаций удваивается. Например, для 2 монет придется выписать всего 4 комбинации. Для 3 монет их уже 8, а для 4 — 16, и вероятность ошибки приближается к 100%. Взгляните на примеры — и сами все поймете:

Задача. В случайном эксперименте симметричную монету бросают 2 раза. Найдите вероятность того, что орлов и решек выпадет одинаковое количество.

Итак, монету бросают два раза. Выпишем все возможные комбинации (O — орел, P — решка):

OO OP PO PP

Итого n = 4 варианта. Теперь выпишем те варианты, которые подходят по условию задачи:

OP PO

Таких вариантов оказалось k = 2. Находим вероятность:

Вероятность для n = 4 и k = 2

Задача. Монету бросают четыре раза. Найдите вероятность того, что решка не выпадет ни разу.

Снова выписываем все возможные комбинации орлов и решек:

OOOO OOOP OOPO OOPP OPOO OPOP OPPO OPPP
POOO POOP POPO POPP PPOO PPOP PPPO PPPP

Всего получилось n = 16 вариантов. Вроде, ничего не забыл. Из этих вариантов нас устраивает лишь комбинация «OOOO», в которой вообще нет решек. Следовательно, k = 1. Осталось найти вероятность:

Вероятность для n = 16 и k = 1

Как видите, в последней задаче пришлось выписывать 16 вариантов. Вы уверены, что сможете выписать их без единой ошибки? Лично я — не уверен. Поэтому давайте рассмотрим второй способ решения.

Специальная формула вероятности

Итак, в задачах с монетами есть собственная формула вероятности. Она настолько простая и важная, что я решил оформить ее в виде теоремы. Взгляните:

Теорема. Пусть монету бросают n раз. Тогда вероятность того, что орел выпадет ровно k раз, можно найти по формуле: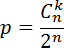

Специальная формула вероятности для задачи B6

Где Cnk — число сочетаний из n элементов по k, которое считается по формуле: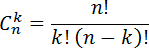

Формула числа сочетани из n элементов по k элементов

Таким образом, для решения задачи с монетами нужны два числа: число бросков и число орлов. Чаще всего эти числа даны прямо в тексте задачи. Более того, не имеет значения, что именно считать: решки или орлы. Ответ получится один и тот же.

На первый взгляд, теорема кажется слишком громоздкой. Но стоит чуть-чуть потренироваться — и вам уже не захочется возвращаться к стандартному алгоритму, описанному выше.

Задача. Монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно три раза.

По условию задачи, всего бросков было n = 4. Требуемое число орлов: k = 3. Подставляем n и k в формулу:

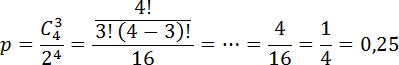
Специальная формула вероятности для n = 4 и k = 3

С тем же успехом можно считать число решек: k = 4 − 3 = 1. Ответ будет таким же.

Задача. Монету бросают три раза. Найдите вероятность того, что решка не выпадет ни разу.

Снова выписываем числа n и k. Поскольку монету бросают 3 раза, n = 3. А поскольку решек быть не должно, k = 0. Осталось подставить числа n и k в формулу:

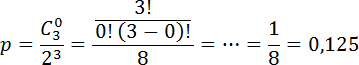
Специальная формула вероятности для n = 3 и k = 0

Напомню, что 0! = 1 по определению. Поэтому C30 = 1.

Задача. В случайном эксперименте симметричную монету бросают 4 раза. Найдите вероятность того, что орел выпадет больше раз, чем решка.

Чтобы орлов было больше, чем решек, они должны выпасть либо 3 раза (тогда решек будет 1), либо 4 (тогда решек вообще не будет). Найдем вероятность каждого из этих событий.

Пусть p1 — вероятность того, что орел выпадет 3 раза. Тогда n = 4, k = 3. Имеем:

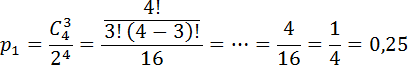
Специальная формула вероятности для n = 4 и k = 3

Теперь найдем p2 — вероятность того, что орел выпадет все 4 раза. В этом случае n = 4, k = 4. Имеем:

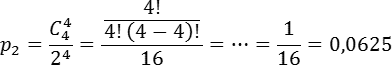
Специальная формула вероятности для n = 4 и k = 4

Чтобы получить ответ, осталось сложить вероятности p1 и p2. Помните: складывать вероятности можно только для взаимоисключающих событий. Имеем:

p = p1 + p2 = 0,25 + 0,0625 = 0,3125

Смотрите также:
  1. Правила комбинаторики в задаче B6
  2. Комбинаторика в задаче B6: легкий тест
  3. Что такое числовая дробь
  4. Задачи B12, сводящиеся к линейным уравнениям
  5. Сложные задачи на проценты
  6. Задача B4 с таблицами: тарифы на интернет