Сегодня мы научимся считать площади фигур в задаче B5 методом узлов. Для начала введем два определения:
Давайте посмотрим, как эти узлы выглядят на конкретной фигуре в задаче B5 из ЕГЭ по математике:
Задача. Найдите площадь четырехугольника изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. Ответ дайте в квадратных сантиметрах.
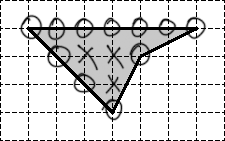
Крестиками обозначены внутренние узлы. Очевидно, их количество n = 3. Кружками обозначены граничные узлы. Их общее количество равно k = 11.
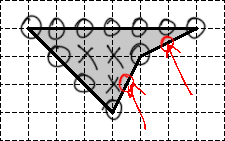
Обратите внимание: под узлами подразумеваются только те точки, которые лежат на пересечении горизонтальных и вертикальных линий нашей сетки. Другими словами, следующие две точки не являются узлами, хотя в них граница фигуры также пересекается с линиями сетки:
Переходим к решению задачи. Для того, чтобы решать задачи B5 ЕГЭ по математике методом узлов, вам потребуется запомнить следующую теорему:
Пусть дана фигура с n внутренними узлами и k граничными узлами. Тогда площадь этой фигуры S считается по формуле:
S = n + 0,5k − 1
Вот так все просто! Главное — запомните, что n — это число внутренних узлов, а k — число граничных узлов.
В нашем случае мы уже подсчитали, что n = 3, k = 11. Подставляем полученные числа в формулу и получаем:
S = 3 + 0,5 · 11 − 1 = 3 + 5,5 − 1 = 7,5
Вот и все решение! Мы получили ответ: площадь четырехугольника равна 7,5. Как видите, задача свелась практически к устному счету. Поэтому обязательно возьмите данный прием на вооружение, ведь велика вероятность того, что на настоящем ЕГЭ по математике вам попадется именно такая задача B5 — площадь фигур на координатной сетке.