Сегодня мы разберем нестандартную задачу B5 на площади из ЕГЭ по математике. В этой задаче требуется найти площадь закрашенного кольца, которое представляет собой две концентрические окружности разных радиусов:
Задача. Найдите площадь S закрашенного кольца, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. В ответе укажите величину S/π.

Как и во всех задачах, для решения нам потребуется формула площади круга:
S = πR2
где R — радиус круга. Это стандартная формула, и ее обязательно надо знать. Но поскольку в задаче фигурируют два круга, то и радиусов будет два. Обозначим внутренний радиус (меньшей окружности) буквой R1, а внешний радиус — R2. Внутренний радиус очень легко считается, он равен двум клеточкам:
R1 = 2 ⇒ R12 = 4
Со вторым радиусом все сложнее. Окружность не проходит через «классические» точки горизонтальной и вертикальной осей, по которым обычно измеряется радиус. Однако на этой окружности есть другие точки, которые лежат в узлах исходной сетки. Отметим эти точки красным:
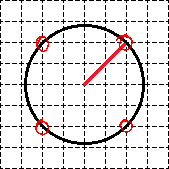
Что дают нам эти точки? Как минимум — визуальное представление того, как выглядит радиус. Для того, чтобы его вычислить, давайте отдельную сетку, на которой отметим центр окружности O и ту точку A на нашей окружности, в которую мы провели радиус. Затем достроим полученный отрезок до прямоугольного треугольника, двигаясь вдоль линий сетки. Получим треугольник OAC с прямым углом C:
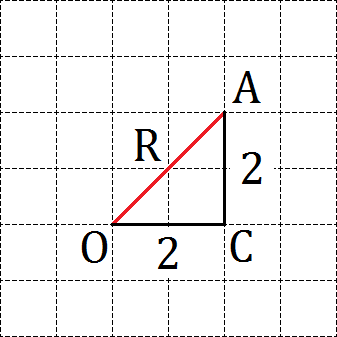
По теореме Пифагора (квадрат гипотенузы равен сумме квадратов катетов) получаем:
R2 = OA2 = OC2 + AC2 = 22 + 22 = 4 + 4 = 8
Итого мы получили:
R22 = 8
Теперь осталось найти площади внешнего и внутреннего кругов, образующих кольцо:
S1 = πR12 = π · 4 = 4π;
S2 = πR22 = π · 8 = 8π.
Поскольку закрашенное кольцо лежит между границами кругов, для нахождения его площади надо из площади большего круга S2 вычесть площадь меньшего круга S1. Получаем:
S = S2 − S1 = 8π − 4π = 4π
Но это еще не ответ! В задаче требуется найти величину S/π. Давайте сосчитаем:
S/π = 4π/π = 4
Вот мы и получили ответ! Как видите, ничего сверхъестественного в этой задаче нет. Достаточно помнить формулу площади круга, а также находить эту площадь через радиус, даже если этот радиус приходится считать через теорему Пифагора.
Надеюсь, этот урок сильно поможет тем, кто всерьез готовится к ЕГЭ по математике. Тем, кто не рассчитывает на то, что им попадутся легкие задачи (в частности, задача B5), а готовится решать в том числе и нестандартные примеры. В общем тренируйтесь — и обязательно сдадите экзамен на отличный балл.:)