В этом коротком уроке мы научимся считать площади фигур без координатной сетки. Здесь не будет никаких клеточек, никаких пересечений и узлов. Будет только система координат и несколько отмеченных чисел.
Как решать такие задачи? В первую очередь, следует отметить, что у нас все-таки есть линии разметки, а точнее проекции точек на оси координат. И именно они потребуются нам для решения задачи. Причем схема будет даже чуть проще, чем при вычислении площадей методом обводки на координатной сетке. Взгляните на задачу:
Задача B5. Найдите площадь треугольника, изображенного на рисунке.
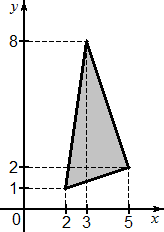
Итак, первый шаг: чертим описанный прямоугольник. Для этого продолжаем линии разметки таким образом, чтобы получилась замкнутая фигура. Это и будет искомый описанный прямоугольник, причем вершины искомой фигуры будут высекать на сторонах этого прямоугольника отдельные отрезки. А значит нам снова нужна формула площади треугольника:
S = 0,5ab
где a и b — катеты (разумеется, речь идет только о прямоугольном треугольнике). А так же пригодится площадь прямоугольника:
S = ab
где a и b — смежные стороны.
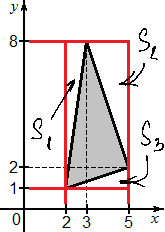
В нашем случае таких треугольников получилось три. Обозначим их S1, S2 и S3. Чтобы сосчитать их площади, нужно сначала найти длину каждого катета. Например, наибольший катер в треугольнике S1 равен a = 8 − 1 = 7, а меньший катет b = 3 − 2 = 1.
Обратите внимание: мы всегда вычитаем из большей абсциссы меньшую, а также из большей ординаты меньшую. Для треугольника S2 верхний катет будет равен a = 5 − 3 = 2, а боковой катет равен b = 8 − 2 = 6. Наконец, для треугольника S3 больший катет будет равен a = 5 − 2 = 3, а меньший катет равен b = 2 − 1 = 1.
Находим площади полученных треугольников:
S1 = 0,5 · 1 · 7 = 3,5;
S2 = 0,5 · 2 · 6 = 6;
S3 = 0,5 · 1 · 3 = 1,5.
Кроме того, нам нужно найти общую площадь описанного прямоугольника. Его стороны равны 7 и 3, а значит площадь равна:
S0 = 7 · 3 = 21.
Осталось выполнить последний шаг. Чтобы найти площадь закрашенной фигуры, нужно из общей площади вычесть площадь дополнительных треугольников, которые мы получили, когда описывали прямоугольник. Получим:
S = S0 − (S1 + S2 + S3) = 21 − (3,5 + 6 + 1,5) = 21 − 11 = 10
Это и является ответом. Площадь закрашенного треугольника равна 10. Как видите, общая схема решения и объем вычислений ничем не отличается от стандартных задач B5 из ЕГЭ по математике, в которых присутствует координатная сетка. Достаточно небольшой тренировки — и вы будете решать эти задачи почти устно.