Этот видео урок посвящен вычислению площадей многоугольников без координатной сетки. Основная трудность решения этой задачи состоит в том, что одна из вершин четырехугольника лежит в начале координат. На практике ничего сложного в этом нет, но почему-то многие ученики в этом путаются и думают, что эта задача решается как-то по-особенному. Давайте посмотрим, как решаются такие задачи B5.
Задача. Найдите площадь четырехугольника, изображенного на рисунке.
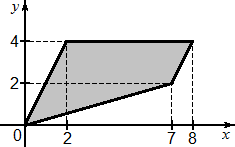
Итак, решаем. В действительности ничего особенного здесь нет. Чертим описанный прямоугольник, причем две из его сторон будут проходить через начало координат. Кроме того, в прямоугольнике есть тупой угол, поэтому спроецируем вершину этого угла на ближайшие стороны описанного прямоугольника. Получили четыре дополнительных фигуры. Обозначим их как S1, S2, S3 и S4. Взгляните на рисунок:
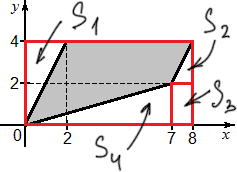
Возвращаемся к решению задачи. Для работы нам потребуется формула площади прямоугольного треугольника:
S = 0,5ab
где a и b — катеты. А так же формула площади прямоугольника со смежными сторонами a и b:
S = ab
Прежде чем перейти, собственно, к решению, необходимо найти стороны данных в задаче треугольников и прямоугольников.
Итак, треугольник S1. Больший его катет равен 4, потому что одна точка лежит в начале координат, а другая точка имеет координаты (0; 4). Вычитаем из ординаты y = 4 ординату y = 0 и получаем 4. Аналогично, второй катет равен 2, так как 2 − 0 = 2.
Далее, у треугольника S2 больший катет равен 2, а меньший 1. У прямоугольника S3 одна сторона равна 1, а другая равна 2, потому что 2 − 0 = 2. Ну, и наконец, в треугольнике S4 один катет уже известен — это 2, а другой катет равен 7 − 0 = 7. Теперь считаем площади:
S1 = 0,5 · 4 · 2 = 4;
S2 = 0,5 · 2 · 1 = 1;
S3 = 2 · 1 = 2;
S4 = 0,5 · 2 · 7 = 7.
Кроме того, нам необходима площадь всего описанного прямоугольника:
S0 = 4 · 8 = 32
Поясню, откуда берутся эти числа. 4 — это одна из сторон прямоугольника, известная нам изначально. А вот вторую сторону нужно найти. Крайняя точка имеет абсциссу x = 8, а вторая точка имеет абсциссу x = 0, получаем 8 − 0 = 8.
Теперь осталось найти площадь закрашенной фигуры, которая и требуется в задаче B5. Для этого нужно из общей площади прямоугольника вычесть сумму площадей всех фигур, входящих в разбиение:
S = S0 − (S1 + S2 + S3 + S4) = 32 − (4 + 1 +2 + 7) = 32 − 14 = 18
Вот и все! Площадь искомого четырехугольника найдена. Она равна 18. Как видите, ничего сложного в задачах B5 из ЕГЭ по математике нет.