В этом видеоуроке я расскажу, как задача о расстоянии между двумя прямыми легко сводится к расстоянию от точки до плоскости. Но для начала напомню несколько фактов из стереометрии.
Пусть скрещивающиеся прямые AB и MN заданы своими направляющими векторами:
AB = (x1, y1, z1);
MN = (x2, y2, z2).
Поскольку прямые скрещиваются, векторы AB и MN не коллинеарны. Следовательно, на них можно построить плоскость. Точнее, множество плоскостей, каждая из которых будет параллельна прямым AB и MN.
Одна из таких плоскостей должна содержать прямую AB. Возьмем на ней произвольную точку T и построим вектор BT:
B = (xB, yB, zB);
T = (x; y; z);
BT = (x − xB, y − yB, z − zB).
Получили три вектора: AB, MN, BT. Составим из них уравнение плоскости через определитель матрицы. При этом координаты векторов станут строчками нашей матрицы:
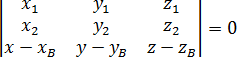
Вот и все! Осталось раскрыть определитель — и уравнение плоскости готово. Эта плоскость содержит прямую AB и параллельна прямой MN. Поэтому расстояние между прямыми AB и MN будет равно расстоянию от плоскости до, скажем, точки M. А расстояние L от точки до плоскости считается по формуле:
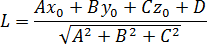
где (x0, y0, z0) — координаты точки, Ax + By + Cz + D = 0 — уравнение плоскости.
А теперь давайте посмотрим, как все это работает на практике: