Дополнительные соображения в задаче C2

30 мая 2011

Метод координат — это, конечно, хороший инструмент, однако у него есть недостаток. Даже два:

1. Иногда приходится много считать. И чем сложнее многогранник — тем больше объем вычислений. Это становится особенно заметно, когда в дело вступают иррациональные координаты и плоскости;
2. К сожалению, в школе этой теме уделяется недостаточно внимания. Проходят что-то в 10 классе — и благополучно забывают. Из-за этого возникают проблемы с оформлением готового решения.

Однако нет ничего невозможного. Если вы освоили метод координат, научились вычислять углы между всевозможными комбинациями прямых и плоскостей, то научиться оформлять свои выкладки — дело пяти минут. А может быть и двух — если эти выкладки немного оптимизировать.

Оптимизация вычислений

Во многих задачах получаются весьма неслабые векторы, координаты которых содержат корни и дроби. От них можно избавиться, если помнить простое правило: при умножении вектора на число a ≠ 0 угол между этим вектором и другими не меняется.

Таким образом, вектор AB = (0,3; 0,5; 1) можно без ущерба для здоровья заменить вектором 10 · AB = (3; 5; 10). Это значительно сократит объем дальнейших вычислений.

Разумеется, это был очень простой пример. Чтобы разобраться с другими тонкостями (например, с корнями), надо выполнить два несложных шага:

1. Избавиться от иррациональности в знаменателе, если она есть. Другими словами, избавляемся от всех корней, которые стоят в знаменателе, путем умножения вектора на этот корень или на сопряженное выражение.
2. Избавиться от иррациональности в числителе и — по возможности — от самих дробей.

Для некоторых эти два правила звучат угрожающе, поэтому разберемся с ними на конкретных примерах. Заодно убедимся, насколько это упрощает решение.

Задача. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁.

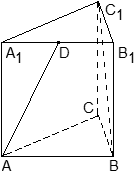
Очевидно, речь идет о косинусе угла между двумя прямыми. Введем стандартную систему координат: начало координат поместим в точку A, единичный отрезок равен AB = 1. Ось x направим вдоль AB, ось z — вдоль AA₁, а ось y расположим так, чтобы плоскость OXY совпадала с плоскостью ABC. Найдем координаты вектора AD:
A = (0; 0; 0) — начало координат.

Точка D — середина отрезка A₁B₁, поэтому нам потребуются точки A₁ и B₁:
A₁ = (0; 0; 1);
B₁ = (1; 0; 1);

D = (0,5; 0; 1) — координаты середины отрезка равны среднему арифметическому координат концов. Итак, находим координаты вектора AD:

AD = (0,5 − 0; 0 − 0; 1 − 1) = (0,5; 0; 1) → (1; 0; 2) — избавились от дробей, умножив координаты вектора на 2.

Теперь найдем координаты вектора BC₁:
B = (1; 0; 0);

Координаты вектора BC₁ также оптимизировали, умножив все на 2. Больше тут ничего не упростить, иррациональность убрать не получится. Остается найти косинус:

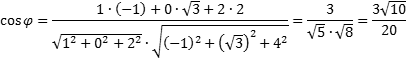
Задача. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E и F — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BF.

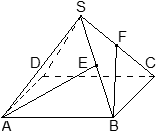
Снова ищем косинус угла между двумя прямыми. Введем систему координат следующим образом: начало координат — точка A, единичный отрезок равен AB = 1. Ось x направим вдоль AB, ось y — вдоль AD, а ось z направим вверх, т.е. перпендикулярно плоскости ABC. Найдем координаты векторов AE и BF.

Координаты точек A = (0; 0; 0) и B = (1; 0; 0) находятся легко. Далее, по условию, точки E и F — середины отрезков SB и SC соответственно, поэтому для нахождения их координат нам потребуются точки C и S:
C = (1; 1; 0);

Откуда взялись корни и как из среднего арифметического получились координаты точек E и F, предлагаю читателям подумать самостоятельно. Подсказка: проведите диагональ основания, высоту и воспользуйтесь теоремой Пифагора.

А мы тем временем найдем и оптимизируем координаты векторов AE и BF:

В обоих случаях координаты вектора умножены на 4, чтобы избавиться от дробей. Осталось найти косинус:

Замечания по оформлению задачи C2

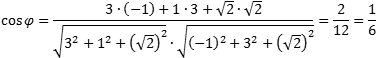
Многие спрашивают: «А примут ли у меня такое решение проверяющие?» Конечно, примут — при условии, что все будет правильно оформлено. Вот основные рекомендации по оформлению:

1. Подробно комментируйте основные моменты решения. Недостаточно просто написать «введем систему координат, как показано на рисунке». Обязательно укажите, где находится начало координат, куда направлены оси и чему равен единичный отрезок.
2. Выписывайте координаты точек, с которыми работаете. Да-да, я знаю, что вы уже тысячу раз чертили кубы и призмы, уже знаете наизусть координаты всех вершин — но проверяющие об этом пока не подозревают! Поэтому начертите еще раз и напишите рядом: A = (0; 0; 0), B = (1; 0; 0) ... — и так все точки, которые вам нужны.
3. Не экономьте на вычислениях. Подставляя числа в формулу для косинуса, напишите эту формулу в исходном виде, затем — с подставленными числами, и только затем проводите вычисления. Это вдвое упростит работу для проверяющего и уменьшит число претензий.
4. Если вы работаете с плоскостями, укажите, почему в формуле Ax + By + Cz + D = 0 коэффициент D принимает конкретные значения (D = 0 или D = 1). В самом деле, почему? Да просто потому, что если плоскость проходит через начало координат, D ≠ 0 не позволит получить верное числовое равенство. Так и напишите — это будет достаточным обоснованием.
5. Внимательно читайте условие задачи. Метод координат дает нам только косинус или синус угла — но не ответ. А что, если требуется тангенс? Обидно, если все решение будет правильным, а ответ — совсем не тот, что надо.

1. Учимся считать угол между плоскостями на примере задачи 14 из профильного ЕГЭ по математике 2016.
2. C2: расстояние между двумя прямыми
3. Тест к уроку «Сложение и вычитание дробей» (легкий)
4. Не пишите единицы измерения в задаче B12
5. Быстрое возведение чисел в квадрат без калькулятора
6. Задача B4: тарифы на сотовую связь