Многие задачи B2 на сложные проценты сводятся к последовательному решению обычных задач на проценты. Главное — научиться выполнять этот переход и, разумеется, грамотно работать с простыми процентами. Сегодня мы посмотрим, как такие задачи можно решать с помощью формулы простого процента — одного из самых эффективных приемов в данной теме.
В этом видеоуроке мы продолжаем изучать сложные задачи на проценты. Но если в прошлый раз мы решали их с помощью коэффициентов, то в этот раз будем работать по стандартной формуле простого процента. У многих учеников сразу возникнет вопрос: как можно считать сложные проценты по формуле простых процентов? Однако ничего сложного в этом нет, и сейчас мы вместе в этом убедимся.
Итак, поехали! Задача:
Задача B2. В июне 1кг помидоров стоит 240 рублей. В июле цена помидоров снизилась на 50%, а в августе — еще на 40% по сравнению с июлем. Сколько рублей стоил 1кг помидоров после снижения цены в августе?
Итак, решаем. Что происходит? Была некая цена х, потом по условию задачи она уменьшилась на 50%, а затем эта новая величина уменьшилась еще на 40%. Как раз для таких ситуаций, когда нам известно исходное значение величины и процент, на который она изменяется, прекрасно подходит формула простого процента. А именно: пусть исходная величина будет х, процент, на который она изменяется — k, а итоговая величина будет y. Можем записать формулу:
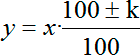
Вот и вся формула. Как применить ее в нашем случае? Давайте для начала узнаем, сколько будут стоить помидоры после понижения стоимости на 50%. Она будет равна:
y1 = x · (100 − 50)/ 100 = 240 · 50/100;
Затем учтем второе понижение, которое произошло в августе, а именно — на 40% по сравнению с июлем. Т.е. уже та величина y1, которую мы получили, уменьшается еще на 40%. Обозначим величину, вновь полученную после очередного уменьшения, как y2. Она будет выражаться по той же самой формуле:
y2 = y1 · (100 − 40)/100 = y1 · 60/100;
Обратите внимание: мы вновь применили формулу простого процента. А поскольку выражение для y1 мы только что нашли, подставляем его в нашу формулу и получаем:
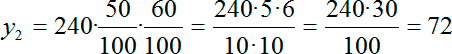
И мы получили, что после всех уменьшений стоимости помидоров итоговая стоимость составила 72 рубля за 1кг. Это и есть ответ к задаче.
В заключении хотел бы обратить ваше внимание на одну тонкость, связанную именно со сложными процентами. Давайте еще раз вернемся к условию задачи. Взгляните: из исходной стоимости 240 рублей сначала уменьшалось на 50%, а затем — еще на 40%.
У многих учеников возникает соблазн сложить 50% и 40% и вместо двух последовательных действий, как мы делали, сделать одно единственное действие, а именно, уменьшить величину 240 сразу на 90%. Делать этого ни в коем случае нельзя. Давайте посмотрим, что произойдет. Попробуем считать так, как считают эти ученики:
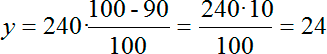
Получается, что при таком подходе, итоговая стоимость, т. е. ответ, будет не 72, а 24. Как видите, возникает ошибка: ответы различаются в 3 раза. При этом правильным будет первый ответ, т. е. 72 рубля.
При вычислении сложных процентов ни в коем случае нельзя складывать проценты напрямую! Это приведет к обидным ошибкам, которые крайне трудно выявляются при проверке.
Причина несоответствия этих ответов заключается в том, что 50% мы считали от 240 рублей, а вот дальнейшие 40% — не от 240 рублей, а уже от той величины, которая получилась в результате уменьшения 240 рублей на 50%. Другими словами, 50% и 40% мы считали от разных величин. Именно поэтому в задаче мы получили больший ответ, чем если бы сразу мы брали 50% и 40% от исходной величины 240 рублей.
Будьте внимательны! На этом моменте погорело очень много людей. Не допускайте таких ошибок. А у меня на этом все. С вами был Павел Бердов. До новых встреч!