Формула простого процента: неизвестно конечное значение

14 ноября 2013

Сегодня мы снова будем решать задачи на проценты, и делать это будем с помощью нашей веселой формулы, которая так и называется: формула простого процента. Давайте я запишу ее:

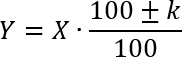
Другими словами, новая величина y всегда выражается из старой величины x через проценты k по указанной формуле. При этом плюс или минус перед числом k ставится в зависимости от того, увеличивается или уменьшается исходная величина x.

Таким образом, все решение задачи B2 на проценты сводится к выявлению трех чисел:

Исходная величина x;
Процентное изменение k;
Итоговая величина y.

Давайте посмотрим, как эта формула работает на реальных задачах. Сегодня таких задач будет сразу две.

Задача 1. В июле 1 кг яблок стоил 80 рублей. В августе яблоки подешевели на 25%. Сколько рублей стоил 1 кг яблок после снижения цены в августе?

Для решения выписываем наши числа — x, k и y. По условию, сначала 1 кг яблок стоил 80 рублей. Т.е. исходная величина x = 80. Затем яблоки подешевели на 25%, т.е. k = 25, причем в формулу это число пойдет с минусом, т.к. величина уменьшается.

В задаче от нас требуется найти итоговое значение y, т.е. стоимость яблок после снижения цены. Итак, запишем нашу формулу простого процента, подставив в нее полученные числа:

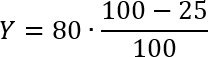
Считаем полученное выражение. В числителе получаем 100 − 25 = 75. Сокращаем со знаменателем и получаем:

y = 80 · 3 : 4 = 20 · 3 = 60

Все легко считается и перемножается. Получаем ответ: y = 60 рублей. Вот мы и нашли, сколько стоил 1 кг яблок после снижения цен в августе. Никаких пропорций и сложных вычислений нам при этом не потребовалось. Как видите, с помощью формулы простого процента многие задачи решаются буквально в пару строчек.

Переходим ко второй задаче.

Задача 2. Магазин покупает учебники по оптовой цене 560 рублей за один учебник. Розничная цена на 60% больше оптовой. Сколько стоит учебник в этом магазине?

Снова выписываем наши числа: x, k и y. Оптовая цена 560 рублей — это исходное значение в нашей формуле, т.е. x = 560. Кроме того, нам известен процент. Т.е. k = 60, причем в формулу процентов число k пойдет с плюсом, ведь по условию задачи новое значение на 60% больше старого.

Ну, и как следует из вопроса, это самое новое значение нам и требуется найти. Что ж, давайте подставим все числа в формулу. Получим:

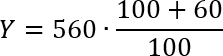
Выполняем сложение в числителе, а затем сокращаем дробь и множитель, стоящий перед дробью:

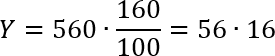
Как видите, мы вообще избавились от дробей. Но получились два двузначных числа, которые надо перемножить. Конечно, можно выполнить умножение столбиком, но давайте мы немного схитрим и перепишем выражение 56 в следующем виде:

y = 56 · 16 = (40 + 16) · 16 = 40 · 16 + 16 · 16 = 640 + 256 = 896

После раскрытия скобок мы получили простые конструкции, которые легко считаются в уме, без всяких столбиков. В результате получилось, что y = 896 — вот такова розничная цена нашего учебника. Это именно то число, которое требуется найти в задаче. Поэтому можем записать ответ: 896.

Данные примеры я специально взял из реальных пробников и ЕГЭ по математике, чтобы на практике показать, насколько упрощается решение многих задач на проценты, если вы используете специальные алгоритмы. Так что очень советую взять на вооружение формулу простого процента.:)

А у меня на этом все. До новых встреч!

Смотрите также: