Сегодня мы вновь разбираем комбинированные задачи, которые включают в себя и задачи на проценты, и вычисление наибольшего/наименьшего значения. Однако, в отличие от предыдущего раза, считать проценты мы будем с помощью пропорции, а не через формулу простых процентов.
Давайте начнем.
Задача 1. Оптовая цена учебника 340 рублей. Розничная цена на 60% выше оптовой. Какое наибольшее число таких учебников можно купить по розничной цене на 5000 рублей?
Первым делом нам надо узнать розничную цену учебника. По условию задачи, розничная цена на 60% выше оптовой, которая в свою очередь равна 340 рублей.
Вводим обозначения: 340 рублей — это 100%. Ну, а x рублей (мы их не знаем) — это те самые 60%, на которые повышается розничная цена. Запишем эти выражения и составим пропорцию:
340 — 100%
x — 60%
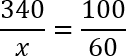
Сокращаем правую дробь на 10 (там получится просто 10/6). Затем воспользуемся основным свойством пропорции: произведение крайних членов равно произведению средних. Получим:
340 · 6 = 10x
Разделим обе стороны этого простейшего уравнения на 10 — получим:
x = 340 · 6 : 10 = 34 · 6 = 180 + 24 = 204
Мы получили, что x = 204 рубля. Это значит, что если исходная оптовая цена была равна 340 рублей, то розничная цена, которая на 60% выше оптовой, равна:
340 + 204 = 544
Итак, мы нашли розничную цену одного учебника. Но в задаче стоит вопрос: какое наибольшее число таких учебников можно купить по розничной цене на 5000 рублей? Чтобы ответить на этот вопрос, давайте разделим 5000 на эти самые 544 рубля, т.е. стоимость одного учебника.
Подозреваю, что это будет 9 с небольшим. Давайте проверим:
544 · 9 = 4500 + 360 + 36 = 4896
Получили 4896 рублей — это чуть-чуть меньше, чем 5000. Следовательно, 9 учебников на 5000 рублей мы купим точно, да еще останется сдача равная:
k = 5000 − 4896 = 104
Разумеется, считать сдачу было необязательно, потому что все, что от нас требуется, мы уже нашли: за 5000 рублей мы можем купить 9 учебников. Плюс сдача, на которую уже ничего не купишь.
Округляем полученное число учебников в меньшую сторону (ведь от нас требуется найти наибольшее число) и получаем просто 9. Это и будет окончательным ответом.
Почему в данной задаче мы округляем в меньшую сторону? Дело в том, что от наст требуется узнать: какое наибольшее число таких учебников можно купить за 5000 рублей? А когда требуется найти наибольшее количество, мы всегда округляем в меньшую сторону. И наоборот: если надо найти наименьшее число, то мы бы округляли в большую.
Все, задача решена. Переходим ко второй задаче.
Задача 2. Кружка стоит 250 рублей. Какое наибольшее число таких кружек можно будет купить на 1000 рублей во время распродажи, когда скидка составляет 30%?
Как видим, задача снова разбивается на 2 части. Сначала надо найти стоимость одной кружки с учетом скидки. Будем искать ее с помощью пропорции.
Если изначально кружка стоила 250 рублей, то эту сумму обозначим за 100%. Далее, нам известна скидка, равная 30%. Ее величина, выраженная в рублях, пусть будет обозначена переменной x. Записываем это и составляем пропорцию:
250 — 100%
x — 30%
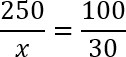
Сокращаем в правой дроби по одному нулю в числителе и знаменателе и получаем 10/3. Теперь снова воспользуемся основным свойством пропорции и перемножим числа крест-накрест. Получим:
250 · 3 = 10 · x
Это простейшее линейное уравнение. Выражаем отсюда x:
x = 250 · 3 : 10 = 25 · 3 = 75
Все легко сокращается и умножается. Получилось, что x = 75 рублей. Итак, мы получили, что во время распродажи скидка составляет x = 75 рублей за кружку. Отлично! Теперь давайте узнаем, сколько будет стоить кружка с учетом этой скидки:
k = 250 − 75 = 175
Получаем, что k = 175 рублей. Именно столько будет стоить кружка с учетом скидки. Ну, и теперь находим: сколько кружек мы можем купить за 10000 рублей. Для этого разделим 1000 рублей на стоимость одной кружки, т.е. 175 рублей. Получим:
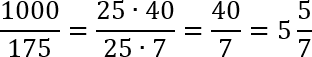
Другими словами, имея в распоряжении 1000 рублей, мы можем купить 5 с небольшим кружек, но не 6. Разумеется, это полный бред, поэтому округляем наше число в меньшую сторону и получаем просто 5 кружек. Потому что дополнительные 5/7 кружки нам никто не продаст.
Да и вообще, в задаче прямо сказано, что надо найти наибольшее число таких кружек. Следовательно, по нашему правилу мы всегда округляем такое число в меньшую сторону. Т.е. ответ — 5 кружек. Все, задача решена.:)
Как видите, задачи B2 на проценты и даже комбинированные задачи на наибольшее/наименьшее значение решаются очень просто. Удачи вам на пробниках и настоящем ЕГЭ. А у меня на этом все. До новых встреч!