Сегодня мы продолжим штурмовать задачи на проценты из ЕГЭ по математике. Но делать это мы будем с помощью специальной формулы, которая так и называется — формула простого процента.
Предлагаю оформить ее в виде теоремы:
Теорема о простом проценте. Пусть нам дана некоторая исходная величина x, дано ее изменение в процентах k, а нужно найти новую величину y, равную результату этих изменений. Тогда новая величина выражается по формуле:
где плюс или минус ставится в зависимости от того, увеличивается величина по условию задачи или уменьшается.
Давайте посмотрим, как эта формула работает на практике.
Задача. Среди 26 000 семей города 1300 семей — многодетные. Какой процент многодетные семьи составляют от всех семей города?
Решаем эту задачу. Согласно нашей формуле, у нас должно быть три числа: x, k и y. Причем x — это исходная величина, т.е. общее количество семей, которых по условию задачи 26 000 штук. Получим:
x = 26 000
Кроме того, известно количество многодетных семей. Всего их 1300, т.е. y = 1300. Осталось разобраться с числом k. В данной задаче оно означает, насколько процентов надо уменьшить исходное количество семей, чтобы получить только многодетные семьи. Что ж, давайте посмотрим. Записываем формулу простого процента:
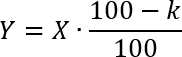
Как видим, при коэффициенте k стоит знак минус, поскольку для получения многодетных семей мы должны убрать из 26 000 семей тех, которые не является многодетными. Вот сейчас и уберем. Подставляем числа в формулу:
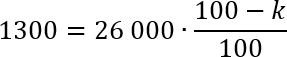
Сразу сокращаем по два нуля у множителя 26 000 и знаменателя 100. Таким образом, дробь лишается знаменателя. Разделим полученное уравнение еще на 10. Другими словами, зачеркнем слева и справа по одному нулю. Получим:
130 = 26 · (100 − k)
Что ж, разделим обе стороны еще на 26. Получим:
100 − k = 5;
k = 100 − 5 = 95.
Итак, мы получили: для того, чтобы из 26 000 семей осталось только 1300 многодетных семей, надо вычесть 95% тех, кто не является многодетными. Следовательно, на многодетные семьи остается лишь 5% от общего числа. Это и есть ответ — то, что нам требовалось найти по условию задачи.
Переходим ко второй задаче.
Задача. Мобильный телефон стоил 16 000 рублей. Через некоторое время цены на эту модель снизили до 12 800 рублей. На сколько процентов была снижена цена?
Эта задача уже гораздо больше подходит для решения по формуле простого процента. Давайте посмотрим: у нас опять фигурируют 3 величины: исходная стоимость x, проценты k и итоговая стоимость y.
Сначала телефон стоил 16 000 рублей. Очевидно, что это начальная цена:
x = 16 000
Затем, после снижения цены телефон стал стоить 12 800 рублей. Это итоговая цена:
y = 12 800
Как видим, от нас снова требуют найти проценты. Что ж, подставляем в формулу и считаем. При этом сама формула простых процентов будет той же самой:
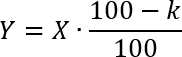
При коэффициенте k будет стоять минус, потому что по условию задачи стоимость телефона снижается. Итак, подставляем наши числа в формулу и записываем уравнение:
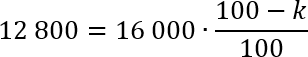
По традиции, сразу сокращаем нули в знаменателе дроби и в числе, стоящем перед дробью. При этом знаменатель дроби исчезнет (поскольку окажется равен единице), а в числителе останется просто 160. Далее разделим обе стороны уравнения на 10, сократив таким образом еще под одному нулю слева и справа. Перепишем полученное уравнение:
1280 = 16 · (100 − k)
Разделим обе стороны уравнения еще на 16 и получим:
100 − k = 1280 : 16
Можно, конечно разделить 1280 : 16 столбиком. Но давайте не будем усложнять себе жизнь, а просто вспомним, что 16 · 16 = 256. Тогда для того, чтобы получить 128, достаточно записать 16 · 8 = 128. Следовательно, имеем:
16 · 16 = 256;
16 · 8 = 128;
16 · 8 · 10 = 1280.
В этом случае наше деление сводится к следующей конструкции:
1280 : 16 = 16 · 8 · 10 : 16 = 8 · 10 = 80
Как видите, все легко сокращается. Переписываем наше уравнение:
100 − k = 80;
k = 100 − 80 = 20.
Итого мобильный телефон подешевел на 20%. Вот и все решение задачи.
Как видите, формула простого процента во многих случаях упрощает решение задачи или, как минимум, делает его более наглядным. Обязательно возьмите эту формулу на вооружение!