Итак, 7 декабря состоялся очередной пробный ЕГЭ по математике. Как и в прошлый раз, ученикам предложили 16 вариантов — все они в ближайшее время будут опубликованы на сайте.
В целом, об экзамене можно сказать следующее:
Сохраняется деление экзамена на варианты без логарифмов (но с производными) и без производных (но с логарифмами). Это связано с тем, что в школах параллельно существуют две программы: по одной из них производные проходят в 10 классе, а логарифмы — в 11, по другой — наоборот. Однако надо готовиться к тому, что уже в январе—феврале 2012 года во всех вариантах будут и логарифмы, и производные;
Новые варианты стали очень похожими друг на друга, условия задач практически совпадают — отличаются лишь числа и, собственно, ответы. С одной стороны, это хорошо, поскольку все ученики находятся в примерно равных условиях. Но с другой стороны, ничего хорошего в этом нет, поскольку настоящие варианты будут существенно (очень существенно!) отличаться друг от друга;
Как ни странно, появились новые задачи, которые ранее вообще не рассматривались — нигде и никогда. В первую очередь это касается теории вероятностей, о чем я расскажу чуть ниже. Подобные «нововведения» сводят на нет всю работу по унификации вариантов.
Выводы: существенных изменений в новых тренировочных вариантах нет. Сами варианты стали более похожими друг на друга, однако в некоторых из них появились новые задачи, с которыми большинство учеников однозначно не справятся.
Теперь разберем конкретные задачи, особенно «новичков» в теории вероятностей.
Согласно спецификациям ЕГЭ по математике, B1 — это задача с практическим содержанием. В нашем случае клиент покупает бензин и получает сдачу. Требуется найти либо размер этой сдачи, либо объем купленного бензина.
Чтобы решить такую задачу, важно знать всего один факт — назовем его законом умножения. Если известна стоимость одного литра
Кроме того, следует раз и навсегда усвоить, что такое сдача. Задумайтесь: когда вы идете в ларек и покупаете бутылку водки за 350 рублей, но в кармане есть лишь купюра в 1000 рублей, то кассир вернет вам 1000 − 350 = 650 рублей. Это и есть сдача — разность между фактической стоимостью покупки и той суммой, которую вы заплатили. Сдача всегда выражается положительным числом.
Задача. На автозаправке клиент отдал кассиру 1000 рублей и залил в бак 22 литра бензина по цене 31 руб. 80 коп. за литр. Какую сдачу клиент должен получить у кассира? Ответ выразите в рублях.
Для начала выразим цену бензина в рублях (без копеек): 31 руб. 80 коп. — это 31,8 рублей.
Итак, один литр стоит 31,8 рублей. Тогда 22 литра стоят 22 · 31,8 = 699,6 рублей. Но клиент отдал кассиру 1000 рублей, поэтому он должен получить сдачу в размере 1000 − 699,6 = 300,4 рубля. Это и есть ответ — переводить число обратно в копейки не требуется.
Задача. На автозаправке клиент отдал кассиру 1000 рублей и попросил залить бензин до полного бака. Цена бензина — 30 руб. 30 коп. за литр. Сдачи клиент получил 303 руб. 10 коп. Сколько литров бензина было залито в бак?
Снова переведем все цены в рубли: 30 руб. 30 коп — это 30,3 рубля; 303 руб. 10 коп. — это 303,1 рубля.
Теперь смотрим на условие задачи. Если клиент отдал кассиру 1000 рублей, а сдачи получил 303,1 рубля, то фактические расходы (цена покупки) составят 1000 − 303,1 = 696,9 рублей.
Поскольку 1 литр бензина стоит 30,3 рубля, то на 696,9 рублей можно купить
Как я и предполагал, в некоторых задачах B3 предлагалось найти площадь многоугольника, заданного координатами своих вершин. При этом координатной сетки на чертеже не было. В других задачах требовалось найти площади секторов.
Задачи с многоугольниками решаются элементарно — достаточно построить описанный прямоугольник (см. урок «Площади многоугольников на координатной сетке»). Как работать с секторами, мы тоже знаем (см. урок «Площадь круга»), правда, в этот раз составители задач предложили более изощренные конструкции.
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 16. Найдите площадь закрашенной фигуры.
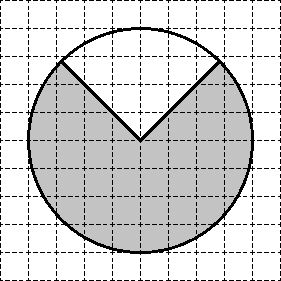
Разрежем круг на 8 равных секторов, как пиццу. Площадь каждого сектора составит
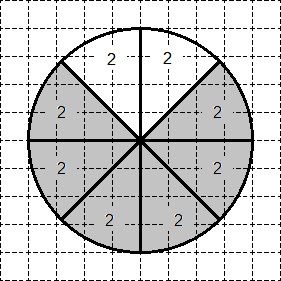
Очевидно, закрашенная часть состоит из 6 таких секторов, поэтому ее площадь равна 6 · 2 = 12.
Задача. Найдите площадь четырехугольника, вершины которого имеют координаты (1; 1), (10; 1), (7; 9), (2; 9)
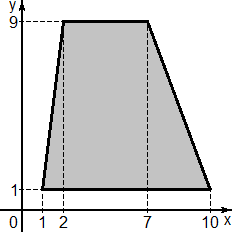
Очевидно, что это трапеция, поэтому можно считать по формуле площади трапеции. Но мы пойдем по традиционному пути: построим описанный прямоугольник и отметим длины всех отрезов. Получим следующую картинку:
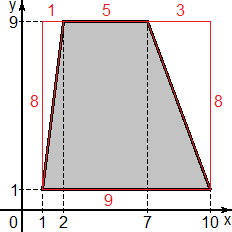
Осталось найти общую площадь
S = 9 · 8 = 72;
S1 = 0,5 · 1 · 8 = 4;
S2 = 0,5 · 3 · 8 = 12;
Sисх = S − (S1 + S2) = 72 − (4 + 12) = 56.
Абсолютно стандартная задача на вычисление тригонометрических функций и работу с координатной окружностью. Большинство ошибок пришлось на варианты, в которых требовалось найти тангенс или котангенс, поскольку в самом конце решения таких задач возникают многоэтажные дроби.
К сожалению, большинство учеников 11 класса до сих пор не умеют работать с многоэтажными дробями. Однако виноват в этом только учитель. Удивительно, но большинство школьных преподавателей математики сами не умеют вычислять такие дроби (см. урок «Сложные выражения с дробями. Порядок действий»).
Лично я считаю, что таких людей нельзя допускать к работе в школе. Учитель математики, который не умеет работать с многоэтажными дробями, должен быть немедленно дисквалифицирован и отправлен на рудники — копать уран.
Если у вас также возникают проблемы с многоэтажными дробями, просто изучите урок, приведенный выше, а затем пройдите прилагающиеся к нему тесты. Поверьте, ничего сложного в этих дробях нет.
Задачи по теории вероятностей всегда отличались разнообразием, но в этот раз составители, похоже, превзошли сами себя. Например, в некоторых вариантах требовалось округлить полученный ответ до сотых. В противном случае получалась бесконечная десятичная дробь. Вот только найти эту дробь большинство учеников сможет лишь при помощи калькулятора, который запрещено использовать на ЕГЭ по математике.
Но округление — это еще полбеды. Гораздо интереснее выглядят задачи про монеты, которые появились в тренировочных вариантах впервые. Для решения таких задач требуется знать, что такое биноминальные коэффициенты — и в ближайшее время мы обязательно рассмотрим эту тему. А пока ограничимся разбором двух конкретных задач из вариантов 1 и 4 (без логарифмов):
Задача. В кармане у Пети было 4 монеты по рублю и 2 монеты по 2 рубля. Петя, не глядя, переложил какие-то три монеты в другой карман. Найдите вероятность того, что обе двухрублевые монеты лежат в одном кармане.
Поскольку обе двухрублевые монеты оказались в одном кармане, то возможны 2 варианта: либо Петя их вообще не перекладывал, либо переложил сразу обе.
В первом случае, когда двухрублевые монеты не перекладывались, придется переложить 3 монеты по рублю. Поскольку всего таких монет 4, число способов это сделать равно числу сочетаний из 4 по 3:
Во втором случае, когда обе двухрублевые монеты были переложены, придется переложить еще одну рублевую монету. Ее надо выбрать из 4 существующих, и число способов так поступить равно числу сочетаний из 4 по 1:
Теперь найдем число способов переложить монеты. Поскольку всего монет 4 + 2 = 6, а выбрать надо лишь 3 из них, общее число вариантов равно числу сочетаний из 6 по 3:
Осталось найти вероятность:
При этом число сочетаний из b по a рассчитывается по формуле, которую обязательно надо знать наизусть:
Задача. В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.
Чтобы пятирублевые монеты лежали в разных карманах, надо переложить только одну из них. Количество способов это сделать равно числу сочетаний из 2 по 1:
Поскольку всего Петя переложил 3 монеты, придется переложить еще 2 монеты по 10 рублей. Таких монет у Пети 4, поэтому количество способов равно числу сочетаний из 4 по 2:
Осталось найти, сколько всего есть вариантов переложить 3 монеты из 6 имеющихся. Это количество, как и в предыдущей задаче, равно числу сочетаний из 6 по 3:
Находим вероятность:
В последнем шаге мы умножали число способов выбрать двухрублевые монеты и число способов выбрать десятирублевые, поскольку данные события независимы.
Отмечу, что сумма вероятностей оказалась равна 0,4 + 0,6 = 1. Действительно, количество монет в обеих задачах совпадает, а две монеты могут лежать либо в одном кармане, либо в разных — третьего не дано.
Этот факт подтверждает правильность ответов, однако решение получилось далеко не тривиальным и требующим очень хорошего знания теории вероятностей. Большинство школьников такими знаниями не обладает.
Задача C1, в которой предлагается решить сложное тригонометрическое уравнение, немного переформулирована и теперь состоит из двух пунктов:
Остальные задачи перекочевали из предыдущего пробного ЕГЭ практически без изменений. Задача C6 осталась такой же легкой и не идет ни в какое сравнение с настоящими C6, которые встречаются в ЕГЭ по математике.