Работа с формулами в задаче B12

13 апреля 2011

Если в задаче B12 дано уравнение, которое содержит несколько переменных, ни одна из которых не рассматривается как «основная» — перед нами задача на работу с формулами. За примерами далеко ходить не надо:

Как видно, формулы могут связывать по три, а то и по четыре переменных. Но решаются такие задачи всегда одинаково.

Взгляните на них: значения переменных, входящих в формулу, указаны прямо в тексте. За исключением одной — ее-то и требуется найти. Таким образом, решение задачи B12 с формулой состоит из трех шагов:

Найти и выписать из текста все известные переменные. Не забудьте перевести все в единую систему измерений. Если одна величина указана в км/ч, а другая — в м/с, то все надо перевести в м/с.
Подставить эти переменные в формулу. Получится уравнение с одной неизвестной.
Решить полученное уравнение — получим ответ.

И еще: прежде чем решать задачу, постарайтесь преобразовать исходную формулу в максимально простой вид — избавляйтесь от корней, дробей и прочего бреда. Это правило распространяется на все задачи ЕГЭ по математике.

Задача. В электросеть включен предохранитель, рассчитанный на силу тока 20 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Сила тока в цепи I связана с напряжением U соотношением: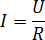

где R — сопротивление прибора. Ответ выразите в Омах.

Для начала перепишем формулу: U = I · R. По условию, нам известно напряжение U = 220 В и сила тока I = 20 А. Ничего переводить в другую систему счисления не надо — все и так переведено. Поэтому находим R:

220 = 20 · R;
R = 11.

Задача. Если наблюдатель находится на небольшой высоте h над поверхностью Земли, то расстояние от него до линии горизонта можно найти по формуле: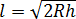

где R = 6400 км — радиус Земли. Найдите наименьшую высоту, с которой должен смотреть наблюдатель, чтобы он видел линию горизонта на расстоянии не менее 6,4 км. Ответ выразите в метрах.

Перепишем формулу: l² = 2Rh. Поскольку нам известны две величины — l = 6,4 км и R = 6400 км — и обе выражены в километрах, можно подставить в формулу и найти h:

6,4² = 2 · 6400 · h;
40,96 = 12 800 · h;
h = 0,0032.

Итак, h = 0,0032 км. Но ответ просят дать в метрах. В одном километре 1000 метров, поэтому имеем:

h = 0,0032 · 1000 = 3,2 м.

Задача. Коэффициент полезного действия некоторого двигателя определяется по формуле:

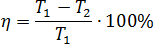
При каком наименьшем значении температуры нагревателя T₁ КПД этого двигателя будет не меньше 70%, если температура холодильника T₂ = 150?

Перепишем формулу, избавившись от дроби: η · T₁ = (T₁ − T₂) · 100. В этой формуле известны КПД η = 70 и температура холодильника T₂ = 150. Подставляем — получаем уравнение относительно T₁:

70 · T₁ = (T₁ − 150) · 100;
70 · T₁ = 100 · T₁ − 15 000;
−30 · T₁ = −15 000;
T₁ = 500.

Задача. В розетку электросети подключены приборы, общее сопротивление которых составляет 60 Ом. Параллельно с ними в розетку хотят подключить обогреватель. Определите наименьшее допустимое сопротивление этого обогревателя, если для нормального функционирования электросети общее сопротивление в ней должно быть не менее 10 Ом.

При этом известно, что при параллельном соединении двух проводников с сопротивлениями R₁ и R₂ их общее сопротивление определяется по формуле: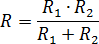

Преобразуем формулу, избавившись от дроби: R · (R₁ + R₂) = R₁ · R₂.

Теперь разберемся с терминологией. Общее сопротивление должно быть не менее 10 Ом — значит, R = 10. Что касается R₁ и R₂, то, не умаляя общности (в силу симметрии формулы), положим R₁ = 60. Соответственно, R₂ — сопротивление обогревателя, которое требуется найти. Имеем:

10 · (60 + R₂) = 60 · R₂;
600 + 10 · R₂ = 60 · R₂;
50 · R₂ = 600;
R₂ = 12.

Задача. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием f = 30 см. Расстояние d₁ от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние d₂ от линзы до экрана — в пределах от 180 до 210 см. Изображения на экране будет четким, если выполнено соотношение: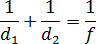

Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы ее изображение на экране было четким. Ответ выразите в сантиметрах.

Снова перепишем формулу, избавившись от дробей:
f · (d₁ + d₂) = d₁ · d₂.

Итак, нам нужно найти d₁. При этом значение f = 30 нам дано, а вот d₂ изменяется от 180 до 210. Получим два уравнения:

30 · (d₁ + 180) = d₁ · 180;
30 · d₁ + 5400 = 180 · d₁;
150 · d₁ = 5400;
d₁ = 36.

30 · (d₁ + 210) = d₁ · 210;
... (решается аналогично предыдущему)
d₁ = 35.

По условию, оба значения d₁ допустимы, поэтому выбираем наименьшее: d₁ = 35.

Небольшое пояснение к задаче с линзами. Многие, увидев волшебную фразу «в пределах от ... до ... », даже не приступают к решению этой задачи. А на самом деле это обычная формула — просто для переменных указаны два значения, поэтому надо составить два уравнения. Получим два значения искомой величины — из них выбираем нужное с учетом ограничений.

Смотрите также: