Линейные уравнения — простейшие конструкции, которые изучаются в школьном курсе математики. Многие задачи B12, которые встречаются в ЕГЭ и выглядят достаточно угрожающе, в итоге сводятся к этим самым линейным уравнениям.
Как правило, линейные уравнения возникают, если:
В любом случае, помните основное правило, одинаково полезное для решения всех задач B12:
Избавляйтесь от дробей и отрицательных степеней в формулах. Если можно умножить — умножайте; можно сократить — сокращайте. Дроби (особенно десятичные) можно записывать только в ответе.
Многие, кто впервые слышит это правило, начинают возмущаться. Мол, к чему такие сложности? Ведь это дополнительные действия, в которых можно допустить еще больше ошибок!
Но статистика неумолима: число ошибок, связанных с преобразованием дробей, меркнет по сравнению с огромным множеством ошибок, которые возникают:
Отдельная проблема — переход от правильной дроби к неправильной и обратно. Подобные операции встречаются во многих задачах ЕГЭ по математике, поэтому настоятельно рекомендую изучить их (см. урок «Что такое числовая дробь»).
В общем, следуйте приведенному выше правилу и не допускайте глупых ошибок. А сейчас посмотрим, как это работает, на конкретных экзаменационных задачах.
Задача. Некоторая компания продает свою продукцию по цене
p = 700 руб. за единицу, переменные затраты на производство одной единицы продукции составляютv = 400 руб., постоянные расходы предприятияf = 800 000 руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле:π (q) = q(p − v) − f.
Определите наименьший месячный объем
производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 1 000 000 руб.
Классическая задача на подстановку переменных в формулу. По условию, нам известно следующее:
π (q) = q(p − v) − f; p = 700; v = 400; f = 800 000.
Требуется, чтобы месячная операционная прибыль
1 000 000 = q(700 − 400) − 800 000;
1 000 000 + 800 000 = q · 300;
300q = 1 800 000;
q = 6000.
Итак, для получения требуемой месячной прибыли необходимо производить 6000 единиц продукции в месяц — это и есть ответ.
Задача. Сила тока в цепи I (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома:
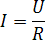
где U — напряжение в вольтах,
R — сопротивление электроприбора в Омах.В электросеть включен предохранитель, который плавится, если сила тока превышает 11 А. Определите, какое минимальное сопротивление (в Омах) должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать.
Избавимся от дробей в формуле, переписав ее в виде
11 · R = 220 ⇒ R = 20.
Итак, сопротивление электроприбора должно быть не менее 20 Ом — это и есть ответ.
Задача. Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой:
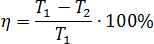
где T1 — температура нагревателя (в градусах Кельвина),
T2 — температура холодильника (в градусах Кельвина).При какой минимальной температуре нагревателя T1 КПД этого двигателя будет не меньше 35%, если температура холодильника
T2 = 260 К? Ответ выразите в градусах Кельвина.
Снова избавляемся от дроби в формуле. Получим:
η · T1 = (T1 − T2) · 100%
Теперь решаем задачу. Нам известны КПД двигателя
35 · T1 = (T1 − 260) · 100;
35T1 =
26 000 = 100T1 − 35T1;
26 000 = 65T1;
T1 = 400 — это ответ.
Задача. При температуре 0 °C рельс имеет длину
l0 = 15 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону:l(t°) = l0(1 + α · t°)
где
α = 1,2 · 10−5 (°C)−1 — коэффициент теплового расширения,t° — температура (в градусах Цельсия). При какой температуре рельс удлинитсяна 6,3 мм? Ответ выразите в градусах Цельсия.
Довольно зверская задача, поскольку и формула, и числа в ней весьма сложные. Для начала выясним, что означает фраза «рельс удлинится
Теперь, когда мы разобрались, что значит «рельс удлинится», можно решить задачу. Имеем:
15 + 6,3 · 10−3 = 15 · (1 + 1,2 · 10−5 · t);
15 + 6,3 · 10−3 =
6,3 · 10−3 =
6,3 · 10−3 · 105 =
6,3 · 102 = 18 · t — избавились от отрицательных степеней;
18t = 630 — получили нормальное уравнение;
t = 35 — решили уравнение.
Как видите, при аккуратном подходе даже самые сложные задачи (например, с рельсами) решаются быстро.
В заключение — небольшое замечание касательно единиц измерения. Вопрос: когда их надо преобразовывать, а когда на это можно забить? В ЕГЭ по математике существует лишь две потенциально «опасные» величины:
Остальные числа — время, температура и другие физические величины — всегда даются в СИ. Исключения существуют, но их единицы, и такие задачи сразу бросаются в глаза.