Эту задачу многие не любят за большой объем вычислений. Да и сам текст задачи довольно-таки громоздкий. Но самое главное — у задачи есть как минимум два различных решения. Какое из них выбрать? Смотрите видео и выбирайте сами.
Задача B4. В среднем за месяц семья расходует в дневное время 140 кВт · ч электроэнергии, а в ночное — 65 кВт · ч. Раньше в квартире был установлен однотарифный счетчик, и всю электроэнергию семья оплачивала по тарифу 2,2 руб. за кВт · ч. Год назад семья установила двухтарифный счетчик, и теперь дневной расход электроэнергии оплачивается по тарифу 2,2 руб. за кВт · ч, а ночной расход — 1,4 руб. за кВт · ч. В течение 12 месяцев режим потребления и тарифы на электроэнергию не менялись. Сколько рублей было сэкономлено за этот период благодаря переходу на двухтарифный счетчик?
Ну, прежде всего, заметим, что у нас есть два варианта: двухтарифный счетчик и однотарифный счетчик. Первым по условию рассматривается однотарифный счетчик. Вот давайте с него и начнем. Для начала рассчитаем, сколько рублей платит наша семья за дневное время в течение одного месяца. Поскольку в дневное время расходуется 140 кВт · ч, а каждый кВт · ч оценивается в 2,2 руб., получим:
140 · 2,2 = 14 · 22 = 308
Кроме того, за этот же месяц есть еще и ночной расход — 65 кВт · ч, их тоже нужно умножить на 2,2 руб. Считаем:
65 · 2,2 = 143
Это расходы в месяц за ночное время. Итого за месяц мы потратим: 308 + 143 = 451 рубль.
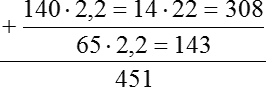
Но по условию задачи от нас требуется узнать, сколько рублей было сэкономлено в период за 12 месяцев, а мы рассчитали только один месяц. Т.е. полученные расходы 451 руб. нужно еще умножить на 12. давайте посчитаем это число столбиком:
451 · 12 = 5412
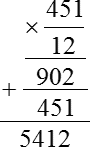
Итого мы затратим 5412 рублей на электроэнергию в течение всех 12 месяцев, при условии, что у нас стоит однотарифный счетчик.
Теперь давайте разберемся с двухтарифным счетчиком. Что мы имеем: потребление энергии ни в коем случае не изменилось, то есть, днем мы все также тратим 140 кВт · ч, а ночью — 65 кВт · ч. Однако дневной расход по условию задачи все также умножается на 2,2 руб., получаем 308 рублей за месяц:
140 · 2,2 = 308
А вот ночной расход умножается не на 2,2, а всего лишь на 1,4 руб. Получим.
65 · 1,4 = 65 + 26 = 91
Итого 91 руб. Итак, если прошлый раз мы тратили за ночь 143 руб., то теперь тратим лишь 91 руб. в месяц. Складываем полученные расходы. Получаем:
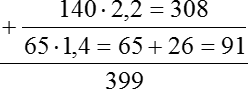
Но это только расходы за месяц, а таких месяцев по условию задачи 12. Поэтому умножаем 399 еще и на 12. Здесь мы не будем считать столбиком, а давайте немножко схитрим:
399 · 12 = (400 – 1) · 12 = 4800 – 12 = 4788
Вот столько денег мы потратим на электричество в течение 12 месяцев, если будем пользоваться двухтарифным счетчиком. Теперь осталось выяснить экономию. То есть, из нашей изначальной цены 5412 руб. нужно вычесть новую цену 4788 руб. Получим:
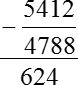
Итого экономия — 624 руб.
Обратите внимание: эта задача несколько отличается от типовых тестовых задач на выбор ответа. Дело в том, что на получение ответа, нам потребовалось рассчитать не просто каждый из исходных вариантов, но еще и вычесть их друг из друга, то есть, как бы сравнить.
В обычных же задачах, которые чаще всего встречаются в ЕГЭ, по идее достаточно бы было рассчитать только один вариант — самый оптимальный. Если бы мы были сенсеями, экстрасенсами, если бы мы сразу видели тот самый вариант, который точно является ответом, то достаточно бы было рассчитать только его, а все остальные даже не смотреть. В данной же задаче всегда придется выполнять полный цикл вычислений. Однако их можно сщественно упростить. Давайте еще раз внимательно посмотрим на наше решение.
Взгляните: при использовании однотарифного счетчика и двухтарифного счетчика. Расходы на дневное употребление энергии не изменилось: было 308 руб. за 140 кВт · ч и осталось 308 руб. за 140 кВт · ч. А вот ночное потребление изменилось: было 143 руб., а стало 91 руб. То есть, вся экономия достигается за снижение расходов на ночное потребление.
Давайте посмотрим, сколько рублей мы экономим за месяц. Вычтем из 143 руб. (расходы по однотарифному счетчику) сумму в 91 руб. (расходы по двухтарифному счетчику). Получим 52 руб. Вот столько денег мы экономим каждый месяц после перехода на двухтарифный счетчик. Экономия:
143 − 91 = 52
А теперь у нас есть 12 месяцев, умножаем их на 52 руб., потому что эта экономия будет возникать каждый из 12-ти месяцев, и получаем (я опять умножу это столбиком):
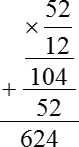
Мы получили тот же самый ответ — 624 руб. Однако объем вычислений оказался существенно меньше. Нам уже не требуется считать общий расход для каждого из вариантов — для двухтарифного и однотарифного счетчиков. Разумеется, при решении реальных задач вы можете пользоваться как стандартным способом (т.е. идти напролом), так и вторым — упрощенным, ускоренным способом. При этом как бы вы ни решали, какой бы путь ни выбрали, при условии правильных вычислений ответ получится один и тот же. В нашем случае — это 624 руб.
Любая математическая задача решает намного быстрее и проще, если ученик не останавливается на первом попавшемся способе и рассмотрит еще несколько подходов.
В этом и состоит сила математики. И если действовать строго по ее правилам, то какой бы алгоритм мы не применяли, ответ окажется одним и тем же. И этот ответ будет правильным. В общем, удачи вам в настоящим ЕГЭ по математике, не ошибайтесь в вычислениях, а у меня на этом все. С вами был Павел Бердов. До новых встреч!
Таким образом, все разнообразие решений сводится к двум вариантам:
Для тех, кому второй вариант покажется слишком сложным, предлагаю самостоятельно решить несколько аналогичных задач B4 — поверьте, вы очень быстро научитесь выделять ту величину, которое действительно влияет на ответ в задаче.