Тригонометрические функции

6 августа 2012

Основная сложность тригонометрических функций состоит в том, что при решении уравнений возникает бесконечное множество корней. Например, уравнение sin x = 0 имеет корни x = πn, n ∈ Z. Ну и как отмечать их на координатной прямой, если таких чисел бесконечно много?

Ответ прост: надо подставлять конкретные значения n. Ведь в задачах B15 с тригонометрическими функциями всегда есть ограничение — отрезок [a; b]. Поэтому для начала берем n = 0, а затем увеличиваем n до тех пор, пока соответствующий корень не «вылезет» за пределы отрезка [a; b]. Аналогично, уменьшая n, очень скоро получим корень, который меньше нижней границы.

Несложно показать, что никаких корней, кроме полученных в рассмотренном процессе, на отрезке [a; b] не существует. Рассмотрим теперь этот процесс на конкретных примерах.

Задача. Найдите точку максимума функции, принадлежащую отрезку [−π/3; π/3]:

y = sin x − 5x sin x − 5cos x + 1

Вычисляем производную:

y’ = (sin x − 5x sin x − 5cos x + 1)’ = ... = cos x − 5x cos x = (1 − 5x) cos x

Затем решаем уравнение:

y’ = 0;
(1 − 5x) cos x = 0;
...
x₁ = 0,2;
x₂ = π/2 + πn, n ∈ Z.

С корнем x = 0,2 все понятно, а вот формула x = π/2 + πn требует дополнительной обработки. Будем подставлять разные значения n, начиная с n = 0.

n = 0 ⇒ x = π/2

Но π/2 > π/3, поэтому корень x = π/2 не входит в исходный отрезок. Кроме того, чем больше n, тем больше x, поэтому нет смысла рассматривать n > 0.

n = −1 ⇒ x = − π/2

Но −π/2 < −π/3 — этот корень тоже придется отбросить. А вместе с ним — и все корни для n < −1.

Получается, что на отрезке [−π/3; π/3] лежит только корень x = 0,2. Отметим его вместе со знаками и границами на координатной прямой:

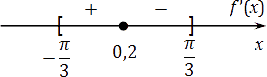
Знаки производной тригонометрической функции

Чтобы удостовериться, что справа от x = 0,2 производная действительно отрицательная, достаточно подставить в производную значение x = π/4. Мы же просто отметим, что в точке x = 0,2 производная меняет знак с плюса на минус, а следовательно, это точка максимума.

Задача. Найдите наибольшее значение функции на отрезке [−π/4; π/4]:

y = 4 tg x − 4x + π − 5

Вычисляем производную:

y’ = (4tg x − 4x + π − 5)’ = 4/cos 2x − 4.

Затем решаем уравнение:

y’ = 0 ⇒ 4/cos 2x − 4 = 0 ⇒ ... ⇒ x = πn, n ∈ Z.

Снова выделим из этой формулы корни, подставляя конкретные n, начиная с n = 0:

n = 0 ⇒ x = 0. Этот корень нам подходит.
n = 1 ⇒ x = π. Но π > π/4, поэтому корень x = π и значения n > 1 надо вычеркнуть.
n = −1 ⇒ x = −π. Но −π < −π/4, поэтому x = −π и n < −1 тоже вычеркиваем.

Из всего многообразия корней остался лишь один: x = 0. Поэтому вычисляем значение функции для x = 0, x = π/4 и x = −π/4. Имеем:

y(0) = 4tg 0 − 4 · 0 + π − 5 = π − 5;
y(π/4) = 4tg π/4 − 4 · π/4 + π − 5 = 1;
y(−π/4) = 4tg (−π/4) − 4 · (−π/4) + π − 5 = ... = 2π − 9.

Теперь заметим, что π = 3,14... < 4, поэтому π − 5 < 4 − 5 < 0 и 2π − 9 < 8 − 9 < 0. Получается одно положительное число и два отрицательных. Мы ищем наибольшее — очевидно, это y = 1.

Заметим, что в последней задаче можно было и не сравнивать числа между собой. Ведь из чисел π − 5, 1 и 2π − 9 в бланк ответов можно записать лишь единицу.

Действительно, как написать в бланке, скажем, число π? А никак. Это важная особенность первой части ЕГЭ по математике, которая значительно упрощает решение многих задач. И работает она не только в B15.

Случай пустого множества решений

Иногда при исследовании функции возникают уравнения, у которых нет корней. В таком случае задача становится еще проще, поскольку остается рассмотреть лишь концы отрезка.

Однако будьте предельно внимательны, поскольку такие задачи встречаются в ЕГЭ крайне редко. Если в процессе решения выясняется, что корней нет, лучше еще раз проверить все выкладки. И только когда убедитесь, что ошибок нет, можно расслабиться: вам досталась легкая задача!

Задача. Найдите наименьшее значение функции на отрезке [−3π/2; 0]:

y = 7sin x − 8x + 5

Сначала находим производную:

y’ = (7sin x − 8x + 5)’ = 7cos x − 8

Попробуем решить уравнение:

y’ = 0 ⇒ 7cos x − 8 = 0 ⇒ cos x = 8/7

Но значения cos x всегда лежат на отрезке [−1; 1], а 8/7 > 1. Поэтому корней нет.

Если корней нет, то и вычеркивать ничего не надо. Переходим к последнему шагу — вычисляем значение функции:

y(−3π/2) = 7sin (−3π/2) − 8 · (−3π/2) + 5 = ... = 12π + 12;
y(0) = 7sin 0 − 8 · 0 + 5 = 5.

Поскольку число 12π + 12 в бланк ответов не записать, остается лишь y = 5.

Смотрите также: