В задаче B15 предлагается исследовать на экстремумы функцию, заданную формулой. Это стандартная задача по математическому анализу, и ее сложность сильно меняется зависимости от рассматриваемой функции: некоторые из них решаются буквально устно, другие же требуют серьезных размышлений.
Прежде чем изучать методы решения, надо усвоить некоторые термины из области математического анализа. Итак, в задаче B15 требуется найти с помощью производной следующие величины:
При этом глобальные экстремумы обычно ищутся не на всей области определения функции, а лишь на некотором отрезке [a; b]. Важно понимать, что глобальный экстремум и значение функции в точке экстремума далеко не всегда совпадают. Поясним это на конкретном примере:
Задача. Найти точку минимума и минимальное значение функции y = 2x3 − 3x2 − 12x + 1 на отрезке [−3; 3].
Сначала найдем точку минимума, для чего вычислим производную:
y’ = (2x3 − 3x2 − 12x + 1)’ = 6x2 − 6x − 12.
Найдем критические точки, решив уравнение y’ = 0. Получим стандартное квадратное уравнение:
y’ = 0 ⇒ 6x2 − 6x − 12 = 0 ⇒ ... ⇒ x1 = −1, x2 = 2.
Отметим эти точки на координатной прямой, добавим знаки производной и ограничения — концы отрезка:
Масштаб картинки не имеет значения. Самое главное — отметить точки в правильной последовательности. Из школьного курса математики известно, что в точке минимума производная меняет знак с минуса на плюс. Отсчет всегда идет слева направо — в направлении положительной полуоси. Поэтому точка минимума одна: x = 2.
Теперь найдем минимальное значение функции на отрезке [−3; 3]. Оно достигается либо в точке минимума (тогда она становится точкой глобального минимума), либо на конце отрезка. Заметим, что на интервале (2; 3) производная всюду положительна, а значит y(3) > y(2), поэтому правый конец отрезка можно не рассматривать. Остались лишь точки x = −3 (левый конец отрезка) и x = 2 (точка минимума). Имеем:
y(−3) = 2(−3)3 − 3(−3)2 − 12(−3) + 1 = −44;
y(2) = 2*23 − 3*22 − 12*2 + 1 = −19.
Итак, наименьшее значение функции достигается на конце отрезка и равно −44.
Ответ: xmin = 2; ymin = −44
Из приведенных рассуждений следует важный факт, о котором многие забывают. Функция принимает максимальное (минимальное) значение не обязательно в точке экстремума. Иногда такое значение достигается на конце отрезка, и производная там не обязана равняться нулю.
Если в задаче B15 требуется найти максимальное или минимальное значение функции f(x) на отрезке [a; b], выполняем следующие действия:
Небольшое пояснение по поводу вычеркивания корней, когда они совпадают с концами отрезка. Их тоже можно вычеркнуть, поскольку на четвертом шаге концы отрезка все равно подставляются в функцию — даже если уравнение f’(x) = 0 не имело решений.
Также следует внимательно читать условие задачи. Когда требуется найти значение функции (максимальное или минимальное), концы отрезка и точки x1, x2, ..., xn подставляются именно в функцию, а не в ее производную.
Задача. Найти наибольшее значение функции y = x3 + 3x2 − 9x − 7 на отрезке [−5; 0].
Для начала найдем производную: y’ = (x3 + 3x2 − 9x − 7)’ = 3x2 + 6x − 9.
Затем решаем уравнение: y’ = 0 ⇒ 3x2 + 6x − 9 = 0 ⇒ ... ⇒ x = −3; x = 1.
Вычеркиваем корень x = 1, потому что он не принадлежит отрезку [−5; 0].
Осталось вычислить значение функции на концах отрезка и в точке x = −3:
y(−5) = (−5)3 + 4·(−5)2 − 9·(−5) − 7 = −12;
y(−3) = (−3)3 + 4·(−3)2 − 9·(−3) − 7 = 20;
y(0) = 03 + 4·02 − 9·0 − 7 = −7.
Очевидно, наибольшее значение равно 20 — оно достигается в точке x = −3.
Теперь рассмотрим случай, когда требуется найти точку максимума или минимума функции f(x) на отрезке [a; b]. Если отрезок не задан, функция рассматривается на своей области определения. В любом случае, схема решения такова:
Вдумчивый читатель наверняка заметит, что для некоторых функций этот алгоритм не работает. Действительно, существует целый класс функций, для которых нахождение точек экстремума требует более сложных выкладок. Однако такие функции в ЕГЭ по математике не встречаются.
Внимательно отнеситесь к расстановке знаков между точками x1, x2, ..., xn. Помните: при переходе через корень четной кратности знак у производной не меняется. Когда ищутся точки экстремума, знаки всегда просматриваются слева направо, т.е. по направлению числовой оси.
Задача. Найти точку максимума функции
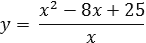
на отрезке [−8; 8].
Найдем производную:
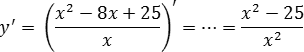
Поскольку это дробно-рациональная функция, приравниваем к нулю производную и ее знаменатель:
y’ = 0 ⇒ x2 − 25 = 0 ⇒ ... ⇒ x = 5; x = −5;
x2 = 0 ⇒ x = 0 (корень второй кратности).
Отметим точки x = −5, x = 0 и x = 5 на координатной прямой, расставим знаки и границы:
Очевидно, что внутри отрезка осталась лишь одна точка x = −5, в которой знак производной меняется с плюса на минус. Это и есть точка максимума.
Еще раз поясним, чем отличаются точки экстремума от самих экстремумов. Точки экстремума — это значения переменных, при которых функция принимает наибольшее или наименьшее значение. Экстремумы — это значения самих функций, максимальные или минимальные в некоторой своей окрестности.
Помимо обычных многочленов и дробно-рациональных функций, в задаче B15 встречаются следующие виды выражений:
С иррациональными функциями проблем, как правило, не возникает. Остальные случаи стоит рассмотреть более подробно.
Основная сложность тригонометрических функций состоит в том, что при решении уравнений возникает бесконечное множество корней. Например, уравнение sin x = 0 имеет корни x = πn, где n ∈ Z. Ну и как отмечать их на координатной прямой, если таких чисел бесконечно много?
Ответ прост: надо подставлять конкретные значения n. Ведь в задачах B15 с тригонометрическими функциями всегда есть ограничение — отрезок [a; b]. Поэтому для начала берем n = 0, а затем увеличиваем n до тех пор, пока соответствующий корень не «вылетит» за пределы отрезка [a; b]. Аналогично, уменьшая n, очень скоро получим корень, который меньше нижней границы.
Несложно показать, что никаких корней, кроме полученных в рассмотренном процессе, на отрезке [a; b] не существует. Рассмотрим теперь этот процесс на конкретных примерах.
Задача. Найти точку максимума функции y = sin x − 5x·sin x − 5cos x + 1, принадлежащую отрезку [−π/3; π/3].
Вычисляем производную: y’ = (sin x − 5x·sin x − 5cos x + 1)’ = ... = cos x − 5x·cos x = (1 − 5x)·cos x.
Затем решаем уравнение: y’ = 0 ⇒ (1 − 5x)·cos x = 0 ⇒ ... ⇒ x = 0,2 или x = π/2 + πn, n ∈ Z.
С корнем x = 0,2 все понятно, а вот формула x = π/2 + πn требует дополнительной обработки. Будем подставлять разные значения n, начиная с n = 0.
n = 0 ⇒ x = π/2. Но π/2 > π/3, поэтому корень x = π/2 не входит в исходный отрезок. Кроме того, чем больше n, тем больше x, поэтому нет смысла рассматривать n > 0.
n = −1 ⇒ x = − π/2. Но −π/2 < −π/3 — этот корень тоже придется отбросить. А вместе с ним — и все корни для n < −1.
Получается, что на отрезке [−π/3; π/3] лежит только корень x = 0,2. Отметим его вместе со знаками и границами на координатной прямой:
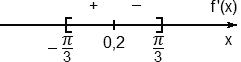
Чтобы удостовериться, что справа от x = 0,2 производная действительно отрицательна, достаточно подставить в y’ значение x = π/4. Мы же просто отметим, что в точке x = 0,2 производная меняет знак с плюса на минус, а следовательно это точка максимума.
Задача. Найти наибольшее значение функции y = 4tg x − 4x + π − 5 на отрезке [−π/4; π/4].
Вычисляем производную: y’ = (4tg x − 4x + π − 5)’ = 4/cos 2x − 4.
Затем решаем уравнение: y’ = 0 ⇒ 4/cos 2x − 4 = 0 ⇒ ... ⇒ x = πn, n ∈ Z.
Выделим из этой формулы корни, подставляя конкретные n, начиная с n = 0:
n = 0 ⇒ x = 0. Этот корень нам подходит.
n = 1 ⇒ x = π. Но π > π/4, поэтому корень x = π и значения n > 1 надо вычеркнуть.
n = −1 ⇒ x = −π. Но π < −π/4, поэтому x = π и n < −1 тоже вычеркиваем.
Из всего многообразия корней остался лишь один: x = 0. Поэтому вычисляем значение функции для x = 0, x = π/4 и x = −π/4.
y(0) = 4tg 0 − 4·0 + π − 5 = π − 5;
y(π/4) = 4tg (π/4) − 4·π/4 + π − 5 = −1;
y(π/4) = 4tg (−π/4) − 4·(−π/4) + π − 5 = ... = 2π − 9.
Теперь заметим, что π = 3,14... < 4, поэтому π − 5 < 4 − 5 = −1 и 2π − 9 < 8 − 9 = −1. Получается одно положительное число и два отрицательных. Мы ищем наибольшее — очевидно, это y = −1.
Заметим, что в последней задаче можно было и не сравнивать числа между собой. Ведь из чисел π − 5, 1 и 2π − 9 в бланк ответов может быть записана лишь единица. Действительно, как написать в бланке, скажем, число π? А никак. Это важная особенность первой части ЕГЭ по математике, которая значительно упрощает решение многих задач. И работает она не только в B15.
Иногда при исследовании функции возникают уравнения, у которых нет корней. В таком случае задача становится еще проще, поскольку остается рассмотреть лишь концы отрезка.
Задача. Найти наименьшее значение функции y = 7sin x − 8x + 5 на отрезке [−3π/2; 0].
Сначала находим производную: y’ = (7sin x − 8x + 5)’ = 7cos x − 8.
Попробуем решить уравнение: y’ = 0 ⇒ 7cos x − 8 = 0 ⇒ cos x = 8/7. Но значения cos x всегда лежат на отрезке [−1; 1], а 8/7 > 1. Поэтому корней нет.
Если корней нет, то и вычеркивать ничего не надо. Переходим к последнему шагу — вычисляем значение функции:
y(−3π/2) = 7sin (−3π/2) − 8·(−3π/2) + 5 = ... = 12π + 12;
y(0) = 7sin 0 − 8·0 + 5 = 5.
Поскольку число 12π + 12 в бланк ответов не записать, остается лишь y = 5.
Вообще говоря, показательная функция — это выражение вида y = ax, где a > 0. Но в задаче B15 встречаются только функции вида y = ex и, в крайнем случае, y = ekx + b. Причина в том, что производные этих функций считаются очень легко:
Все остальное абсолютно стандартно. Разумеется, настоящие функции в задачах B15 выглядят более сурово, но схема решения от этого не меняется. Рассмотрим пару примеров, выделяя лишь основные моменты решения — без основательных рассуждений и комментариев.
Задача. Найти наименьшее значение функции y = (x2 − 5x + 5)ex − 3 на отрезке [−1; 5].
Производная: y’ = ((x2 − 5x + 5)ex − 3)’ = ... = (x2 − 3x)ex − 3 = x(x − 3)ex − 3.
Находим корни: y’ = 0 ⇒ x(x − 3)ex − 3 = 0 ⇒ ... ⇒ x = 0; x = 3.
Оба корня лежат на отрезке [−1; 5]. Осталось найти значение функции во всех точках:
y(−1) = ((−1)2 − 5·(−1) + 5)e− 1 − 3 = ... = 11·e−4;
y(0) = (02 − 5·0 + 5)e0 − 3 = ... = 5·e−3;
y(3) = (32 − 5·3 + 5)e3 − 3 = ... = −1;
y(5) = (52 − 5·5 + 5)e5 − 3 = ... = 5·e2.
Из четырех полученных чисел в бланк можно записать лишь y = −1. К тому же, это единственное отрицательное число — оно и будет наименьшим.
Задача. Найти наибольшее значение функции y = (2x − 7)·e8 − 2x на отрезке [0; 6].
Производная: y’ = ((2x − 7)·e8 − 2x)’ = ... = (16 − 4x)·e8 − 2x = 4(4 − x)·e8 − 2x.
Находим корни: y’ = 0 ⇒ 4(4 − x)·e8 − 2x = 0 ⇒ x = 4.
Корень x = 4 принадлежит отрезку [0; 6]. Ищем значения функции:
y(0) = (2·0 − 7)e8 − 2·0 = ... = −7·e8;
y(4) = (2·4 − 7)e8 − 2·4 = ... = 1;
y(6) = (2·6 − 7)e8 − 2·6 = ... = 5·e−4.
Очевидно в качестве ответа может выступать лишь y = 1.
По аналогии с показательными функциями, в задаче B15 встречаются только натуральные логарифмы, поскольку их производная легко считается:
Таким образом, производная всегда будет дробно-рациональной функцией. Остается лишь приравнять эту производную и ее знаменатель к нулю, а затем решить полученные уравнения.
Для поиска максимального или минимального значения логарифмической функции помните: натуральный логарифм обращается в «нормальное» число только в точках вида en. Например, ln 1 = ln e0 = 0 — это логарифмический ноль, и чаще всего решение сводится именно к нему. В остальных случаях «убрать» знак логарифма невозможно.
Задача. Найти наименьшее значение функции y = x2 − 3x + ln x на отрезке [0,5; 5].
Считаем производную:
Находим нули производной и ее знаменателя:
y’ = 0 ⇒ 2x2 − 3x + 1 = 0 ⇒ ... ⇒ x = 0,5; x = 1;
x = 0 — тут решать нечего.
Из трех чисел x = 0, x = 0,5 и x = 1 внутри отрезка [0,5; 5] лежит только x = 1, а число x = 0,5 является его концом. Имеем:
y(0,5) = 0,52 − 3·0,5 + ln 0,5 = ln 0,5 − 1,25;
y(1) = 12 − 3·1 + ln 1 = −2;
y(5) = 52 − 3·5 + ln 5 = 10 + ln 5.
Из полученных трех значений лишь y = −2 не содержит знака логарифма — это и будет ответ.
Задача. Найти наибольшее значение функции y = ln(6x) − 6x + 4 на отрезке [0,1; 3].
Вычисляем производную:
Выясняем, когда производная или ее знаменатель равны нулю:
y’ = 0 ⇒ 1 − 6x = 0 ⇒ x = 1/6;
x = 0 — уже решено.
Вычеркиваем число x = 0, поскольку оно лежит за пределами отрезка [0,1; 3]. Считаем значение функции на концах отрезка и в точке x = 1/6:
y(0,1) = ln(6·0,1) − 6·0,1 + 4 = ln 0,6 + 3,4;
y(1/6) = ln(6·1/6) − 6·1/6 + 4 = ln 1 + 3 = 3;
y(3) = ln(6·3) − 6·3 + 4 = ln 18 − 14.
Очевидно, только y = 3 может выступать в качестве ответа — остальные значения содержат знак логарифма и не могут быть записаны в бланк ответов.