Для тех, кто уже научился решать задачи B15 с логарифмами (см. «Специфика работы с логарифмами в задаче B15»), есть более продвинутые инструменты. С их помощью ответ находится буквально за секунды. Не верите? Читайте дальше.
Первая фишка идеально подходит для простых функций, в которых стоит только один логарифм. Она работает в тех задачах, где требуется найти значение функции (а не точку экстремума). В этом случае:
Выражение под знаком логарифма должно равняться единице. Потому что ln 1 = 0.
Откуда берется это требование? А вы попробуйте сосчитать, например, ln 2 или ln 0,5. В обоих случаях получится иррациональное число, которое нельзя записать в ответ. И только ln 1 = 0 — нормальное число.
Задача. Найдите наибольшее значение функции на отрезке [−1,5; 0]:
y = 3ln(x + 2) − 3x + 10.
Как видим, в задаче есть ровно один логарифм: ln(x + 2). Его аргумент должен быть равен единице:
x + 2 = 1;
x = −1.
Поскольку нас просят найти наибольшее значение функции, число x = −1 — не что иное как точка максимума. Находим значение функции в этой точке:
y (−2) = 3ln(−1 + 2) − 3 · (−1) + 10 = 3 · 0 + 3 + 10 = 13
Задача. Найдите наименьшее значение функции на отрезке [11/12; 13/12]:
y = 3x2 − 11x + 5ln x + 7
Снова приравниваем аргумент логарифма к единице:
x = 1
Подставляем это число в исходную функцию:
y (1) = 3 · 12 − 11 · 1 + 5 ln 1 + 7 = 3 − 11 + 5 · 0 + 7 = −1
Вдумчивый читатель возразит, мол, существует замечательное число e ≈ 2,7. И для него ln e = 1, ln e2 = 2 и т.д. Но составитель задач должен быть настоящим маньяком, чтобы «втиснуть» в функцию это число. Встреть такую задачу на ЕГЭ почти нереально.
Если функция содержит сразу несколько логарифмов, их надо объединить по правилам сложения и вычитания — см. «Основные свойства логарифмов».
Задача. Найдите наименьшее значение функции на отрезке [0,2; 1,2]:
y = 2x2 − 5x + ln (12x) − 7 − ln 12
Для начала объединим логарифмы и перепишем исходную функцию:
ln (12x) − ln 12 = ln (12x : 12) = ln x;
y = 2x2 − 5x + ln x − 7.
Остался один логарифм. Его аргумент должен быть равен единице:
x = 1
Находим значение функции в точке x = 1 — это и будет наименьшее значение:
y (1) = 2 · 12 − 5 · 1 + ln 1 − 7 = 2 − 5 + 0 − 7 = −10
Если логарифм умножается на другую функцию, приведенные выше правила не работают. Взгляните на пример:
y = (x − 5) · ln x
Эта функция будет нормальным числом при x = 1, поскольку логарифм обнулится, и при x = 5, поскольку обнулится множитель (x − 5).
Такие задачи считаются только по стандартной схеме, через производную. Кстати, логарифм всегда будет только натуральный, потому что у него нормальная производная:
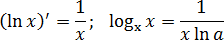
Задача. Найдите наименьшее значение функции на отрезке [1; 5]:
y = x · (ln x − ln 2 − 1)
Итак, логарифм умножается на другую функцию. Значит, специальные правила бесполезны — работаем по стандартной схеме. Считаем производную:
y´ = (x · (ln x − ln 2 − 1))´ = (x)´ · (ln x − ln 2 − 1) + x · (ln x − ln 2 − 1)´ = ln x − ln 2 − 1 + 1 = ln x − ln 2
Производная функции вполне адекватна. Приравниваем ее к нулю:
ln x − ln 2 = 0;
ln x = ln 2;
x = 2.
Точка x = 2 ∈ [1; 5], значит у нас три числа: 1; 2; 5. Подставляем их в исходную функцию:
y (1) = 1 · (ln 1 − ln 2 − 1) = −ln 2 − 1;
y (2) = 2 · (ln 2 − ln 2 − 1) = −2;
y (5) = 5 · (ln 5 − ln 2 − 1) = 5 · (ln (5 : 2) − 1) = 5 · (ln 2,5 − 1).
Первое и последнее число нам явно не подходят, поскольку их нельзя записать в ответ. Остается единственное значение функции: −2.
В заключение, еще раз перечислю основные моменты: