Сегодня мы продолжаем изучать задачи на наибольшее и наименьшее значение из ЕГЭ по математике. Теперь перед нами довольно серьезная задача, в которой придется использовать формулу производной частного. Итак:
Задача B15. Найдите наименьшее значение функции на отрезке [0; 1]:
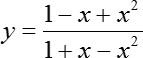
В первую очередь вспомним: как вообще решаются задачи такого типа, в которых требуется найти наименьшее или наибольшее значение функции? Решение таких задач состоит из нескольких этапов:
Практика показывает, что, как правило, мы получаем только один корень. В этом корне как раз и возникает ответ ко всей задаче, т. е. наименьшее или наибольшее значение функции, но бывают исключения, поэтому концы отрезка тоже нужно подставлять.
Помните: далеко не всегда наибольшее или наименьшее значение функции достигается в точках максимума или минимума. Вполне возможно, что наибольшее или наименьшее значение возникнет на концах отрезка.
Давайте применим этот четырехступенчатый алгоритм к нашей функции:
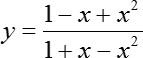
Поскольку перед нами дробь, то сейчас нужно будет считать производную дроби. Напомню, что производная частного считается по следующей формуле:
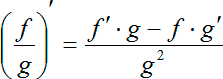
Применяем это правило для нашей функции. Считаем производную:
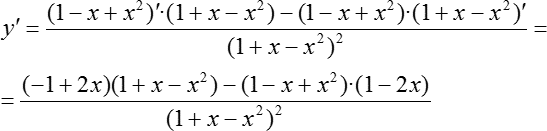
Разбираемся с числителем. Первая мысль, которая возникает — раскрыть все скобки и привести слагаемые. Но это не самый оптимальный вариант, потому что есть более красивый и быстрый путь. Давайте заметим: первая скобка — (−1 + 2х), а последняя скобка — (1 − 2х), т. е. эти скобки противоположны друг другу. С помощью минуса мы можем поменять знаки. Смотрите:
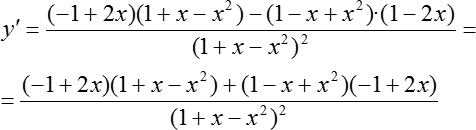
Теперь мы видим, что в первом и во втором слагаемом есть общий множитель, а именно — (−1 + 2х). Давайте вынесем этот общий множитель за скобку:
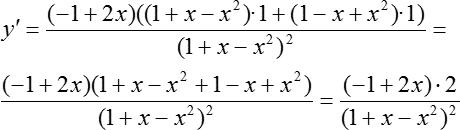
Готово! Производная частного найдена.
Мы получили довольно простую конструкцию, которая является нашей производной. Переходим ко второму шагу: приравниваем эту конструкцию к нулю и считаем корни:
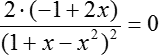
Дробь равна нулю, когда ее числитель равен нулю, а знаменатель отличен от нуля. Множитель «2» в этом случае не может быть равен нулю, поэтому:
−1 + 2x = 0;
x = 1/2.
Разумеется, при таком х знаменатель будет отличен от нуля, потому что при подстановке у нас получится 5/4, что явно не является нулем. Следовательно, x = 1/2 является единственным корнем (когда производная равна нулю).
Переходим к третьему шагу: отбираем корни, лежащие на отрезке [0; 1]. В нашем случае корень 1/2 действительно принадлежит этому отрезку:
1/2 ∈ [0; 1]
Следовательно, мы смело можем переходить к четвертому шагу и подставлять все три числа, а именно — корень 1/2 и концы отрезка 0 и 1 — в исходную функцию:
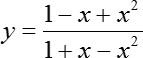
Давайте подставлять. Начнем с самого сложного — числа x = 1/2. Считаем:
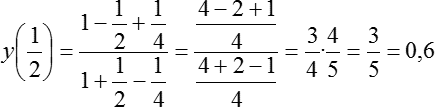
Теперь подставляем x = 0:
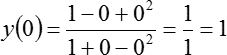
Наконец подставляем х = 1, т. е. правый конец отрезка:
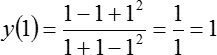
У нас получилось то же самое число.
Итого у нас получилось три значения функции, т. е. три кандидата на ответ. На самом деле их два, потому что два последних совпадают. Получаем два числа: y = 0,6 и y = 1.
Давайте вернемся к исходному условию задачи, посмотрим, что от нас требуется. А от нас требуется найти наименьшее значение функции. Т. е. из двух полученных чисел — 0,6 и 1 — нужно выбрать наименьшее. Очевидно, что ответом будет y = 0,6. Все, задача решена.
Единственный момент, на который я бы хотел обратить ваше внимание, заключается в следующем. Давайте еще раз вернемся к нашему алгоритму:
На четвертом пункте мы считаем значение функции не только в нулях производной, но еще и на концах отрезка. У многих учеников возникнет вопрос: зачем вообще считать значение функции на концах отрезка, если и так ясно, что наибольшее или наименьшее значение принимается в нулях производной?
Хочу вас предупредить: это очень частое и ошибочное заблуждение! Потому что при наличии любых ограничений отнюдь не всегда наибольшее или наименьшее значение функции достигается в точке максимума или минимума.
Рассмотрим простой пример. Взгляните на такую функцию:
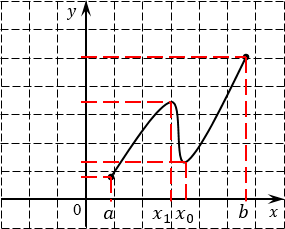
Ну и где достигается наибольшее и наименьшее значение этой функции, а где — точки максимума и минимума? Точка минимума очевидна — назовем ее x0. В ней убывание функции сменяется возрастанием. И напротив, точка x1 является точкой максимума, потому что в ней возрастание функции сменяется убыванием.
Однако максимальное значение функции достигается отнюдь не в точке x = x1, а на конце отрезка — именно в точке x = b функция поднимается на максимальную высоту. И наоборот: наименьшее значение достигается именно в точке x = a, а никак не в точке минимума x = x0. Поэтому помните: наибольшее и наименьшее значение функции на отрезке совсем необязательно достигается в точках максимума и минимума. Это значение также может достигаться на концах отрезка.
Далеко не всегда наибольшее или наименьшее значение функции достигается в точке экстремума! Очень часто это происходит на концах отрезка.
Применительно к задачам из ЕГЭ по математике можно сказать следующее: такие графики функций, когда наибольшее значение оказывается на концах отрезка, в настоящих задачах из ЕГЭ встречаются крайне редко. Однако они все-таки существуют, в том числе в настоящем ЕГЭ, а не только в пробниках. Поэтому будет очень обидно, если, зная, как решается задача, вы, тем не менее, допустите в ней ошибку — просто потому, что не проверите концы отрезка.
Удачи вам в подготовке к ЕГЭ по математике, оставайтесь с нами, решайте задачи, смотрите видеоуроки — и никакие (даже самые сложные!) задачи по математике вам будут не страшны. А у меня на сегодня все.:)