В задаче B7 дается некоторое выражение, которое нужно упростить. В результате должно получиться обычное число, которое можно записать в бланке ответов. Все выражения условно делятся на три типа:
Показательные и логарифмические выражения в чистом виде практически не встречаются. Однако знать, как они вычисляются, совершенно необходимо.
В целом, задача B7 решается достаточно просто и вполне под силу среднему выпускнику. Отсутствие четких алгоритмов компенсируется в ней стандартностью и однообразностью. Научиться решать такие задачи можно просто за счет большого количества тренировок.
Подавляющее большинство задач B7 содержат логарифмы в том или ином виде. Эта тема традиционно считается сложной, поскольку ее изучение приходится, как правило, на 11 класс — эпоху массовой подготовки к выпускным экзаменам. В результате многие выпускники имеют весьма смутное представление о логарифмах.
Но в этой задаче никто и не требует глубоких теоретических познаний. Нам будут встречаться лишь самые простые выражения, которые требуют незамысловатых рассуждений и вполне могут быть освоены самостоятельно. Ниже приведены основные формулы, которые надо знать, чтобы справиться с логарифмами:
Кроме того, надо уметь заменять корни и дроби на степени с рациональным показателем, иначе в некоторых выражениях выносить из под знака логарифма будет просто нечего. Формулы замены:
Задача. Найти значения выражений:
log6 270 − log6 7,5
log5 775 − log5 6,2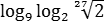
Первые два выражения преобразуются как разность логарифмов:
log6 270 − log6 7,5 = log6 (270 : 7,5) = log6 36 = 2;
log5 775 − log5 6,2 = log5 (775 : 6,2) = log5 125 = 3.
Для вычисления третьего выражения придется выделять степени — как в основании, так и в аргументе. Для начала найдем внутренний логарифм:
Затем — внешний:
Конструкции вида loga logb x многим кажутся сложными и непонятыми. А между тем, это всего лишь логарифм от логарифма, т.е. loga (logb x). Сначала вычисляется внутренний логарифм (положим logb x = c), а затем внешний: loga c.
Будем называть показательным выражением любую конструкцию вида ak, где числа a и k — произвольные постоянные, причем a > 0. Методы работы с такими выражениями достаточно просты и рассматриваются на уроках алгебры 8-го класса.
Ниже приведены основные формулы, которые обязательно надо знать. Применение этих формул на практике, как правило, не вызывает проблем.
Если встретилось сложное выражение со степенями, и не понятно, как к нему подступиться, используют универсальный прием — разложение на простые множители. В результате большие числа в основаниях степеней заменяются простыми и понятными элементами. Затем останется лишь применить указанные выше формулы — и задача будет решена.
Задача. Найти значения выражений: 79 · 311 : 218, 247 : 36 : 165, 306 : 65 : 252.
Решение. Разложим все основания степеней на простые множители:
79 · 311 : 218 = 79 · 311 : (7 · 3)8 = 79 · 311 : (78 · 38) = 79 · 311 : 78 : 38 = 7 · 33 = 189.
247 : 36 : 165 = (3 · 23)7 : 36 : (24)5 = 37 · 221 : 36 : 220 = 3 · 2 = 6.
306 : 65 : 252 = (5 · 3 · 2)6 : (3 · 2)5 : (52)2 = 56 · 36 · 26 : 35 : 25 : 54 = 52 · 3 · 2 = 150.
Если знать формулы, то все показательные и логарифмические выражения решаются буквально в одну строчку. Однако в задаче B7 степени и логарифмы могут объединяться, образуя довольно неслабые комбинации.
Из определения логарифма вытекают две формулы, которые постоянно встречаются в реальных задачах. Эти формулы позволяют заменить знак логарифма нормальными числами:
В чистом виде они, как правило, не встречаются, поэтому общая схема решения комбинированных задач выглядит так:
На первый взгляд эта схема кажется громоздкой и далеко не оптимальной. Но стоит немного потренироваться — и комбинированные задачи будут решаться за несколько секунд. Особо продвинутые решают их устно.
Задача. Найти значения выражений:
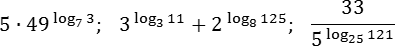
Будем действовать по схеме. Для первого выражения все очевидно:
Для второго выражения заметим, что
Поэтому имеем:
Аналогично поступим с третьим выражением:
В результате получим: