Сегодня мы научимся решать самые простые логарифмические уравнения, где не требуются предварительные преобразования и отбор корней. Но если научиться решать такие уравнения, дальше будет намного проще.
Простейшее логарифмическое уравнение — это уравнение вида loga f (x) = b, где a, b — числа (a > 0, a ≠ 1), f (x) — некоторая функция.
Отличительная особенность всех логарифмических уравнений — наличие переменной x под знаком логарифма. Если изначально в задаче дано именно такое уравнение, оно называется простейшим. Любые другие логарифмические уравнения сводятся к простейшим путем специальных преобразований (см. «Основные свойства логарифмов»). Однако при этом надо учитывать многочисленные тонкости: могут возникнуть лишние корни, поэтому сложные логарифмические уравнения будут рассмотрены отдельно.
Как решать такие уравнения? Достаточно заменить число, стоящее справа от знака равенства, логарифмом по тому же основанию, что и слева. Затем можно избавиться от знака логарифма. Получим:
loga f (x) = b ⇒ loga f (x) = loga ab ⇒ f (x) = ab
Получили обычное уравнение. Его корни являются корнями исходного уравнения.
Зачастую логарифмические уравнения, которые внешне выглядят сложно и угрожающе, решаются буквально в пару строчек без привлечения сложных формул. Сегодня мы рассмотрим именно такие задачи, где все, что от вас потребуется — аккуратно свести формулу к канонической форме и не растеряться при поиске области определения логарифмов.
Сегодня, как вы уже наверняка догадались из названия, мы будем решать логарифмические уравнения по формулам перехода к канонической форме. Основной «фишкой» данного видеоурока будет работа со степенями, а точнее, вынесение степени из основания и аргумента. Давайте рассмотрим правило:
Аналогичным образом можно вынести степень и из основания:
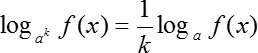
Как видим, если при вынесении степени из аргумента логарифма у нас просто появляется дополнительный множитель спереди, то при вынесении степени из основания — не просто множитель, а перевернутый множитель. Это нужно помнить.
Наконец, самое интересное. Данные формулы можно объединить, тогда мы получим:
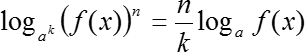
Разумеется, при выполнении данных переходов существуют определенные подводные камни, связанные с возможным расширением области определения или, наоборот, сужением области определения. Судите сами:
log3 x2 = 2 ∙ log3 x
Если в первом случае в качестве x могло стоять любое число, отличное от 0, т. е. требование x ≠ 0, то во втором случае нас устроят лишь x, которые не только не равны, а строго больше 0, потому что область определения логарифма состоит в том, чтобы аргумент был строго больше 0. Поэтому напомню вам замечательную формулу из курса алгебры 8—9 класса:
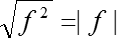
То есть, мы должны записать нашу формулу следующим образом:
log3 x2 = 2 ∙ log3 |x|
Тогда никакого сужения области определения не произойдет.
Однако в сегодняшнем видеоуроке никаких квадратов не будет. Если вы посмотрите на наши задачи, то увидите только корни. Следовательно, применять данное правило мы не будем, однако его все равно необходимо держать в голове, чтобы в нужный момент, когда вы увидите квадратичную функцию в аргументе или основании логарифма, вы вспомните это правило и все преобразования выполните верно.
Итак, первое уравнение:
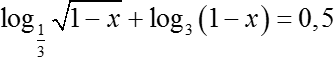
Для решения такой задачи предлагаю внимательно посмотреть на каждое из слагаемых, присутствующих в формуле.
Давайте перепишем первое слагаемое в виде степени с рациональным показателем:
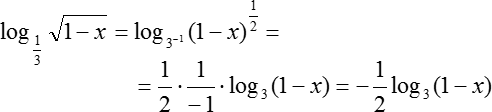
Смотрим на второе слагаемое: log3 (1 − x). Здесь делать ничего не нужно, здесь все уже преобразовании.
Наконец, 0, 5. Как я уже говорил в предыдущих уроках, при решении логарифмических уравнений и формул очень рекомендую переходить от десятичных дробей к обычным. Давайте так и сделаем:
0,5 = 5/10 = 1/2
Перепишем наше исходную формулу с учетом полученных слагаемых:
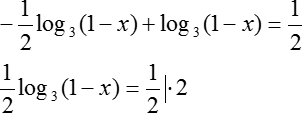
log3 (1 − x) = 1
Теперь переходим к канонической форме:
log3 (1 − x) = log3 3
Избавляемся от знака логарифма, приравнивая аргументы:
1 − x = 3
−x = 2
x = −2
Все, мы решили уравнение. Однако давайте все-таки подстрахуемся и найдем область определения. Для этого вернемся к исходной формуле и посмотрим:
1 − x > 0
−x > −1
x < 1
Наш корень x = −2 удовлетворяет это требование, следовательно, x = −2 является решением исходного уравнения. Вот теперь мы получили строгое четкое обоснование. Все, задача решена.
Переходим ко второй задаче:
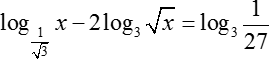
Давайте разбираться с каждым слагаемым отдельно.
Выписываем первое:
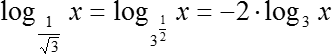
Первое слагаемое мы преобразовали. Работаем со вторым слагаемым:
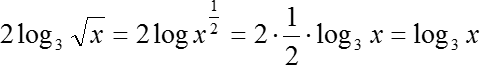
Наконец, последнее слагаемое, которое стоит справа от знака равенства:
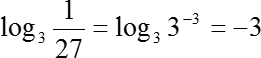
Подставляем полученные выражения вместо слагаемых в полученной формуле:
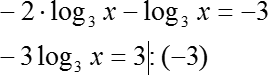
log3 x = 1
Переходим к канонической форме:
log3 x = log3 3
Избавляемся от знака логарифма, приравнивая аргументы, и получаем:
x = 3
Опять же, давайте на всякий случай подстрахуемся, вернемся к исходному уравнению и посмотрим. В исходной формуле переменная x присутствует только в аргументе, следовательно,
x > 0
Во втором логарифме x стоит под корнем, но опять же в аргументе, следовательно, корень должен быть больше 0, т. е. подкоренное выражение должно быть больше 0. Смотрим на наш корень x = 3. Очевидно, что он удовлетворяет это требование. Следовательно, x = 3 является решением исходного логарифмического уравнения. Все, задача решена.
Ключевых моментов в сегодняшнем видеоуроке два:
1) не бойтесь преобразовывать логарифмы и, в частности, не бойтесь выносить степени за знак логарифма, при этом помните нашу основную формулу: при вынесении степени из аргумента она выносится просто без изменений как множитель, а при вынесении степени из основания эта степень переворачивается.
2) второй момент связан с само канонической формой. Переход к канонической форме мы выполняли в самом конце преобразования формулы логарифмического уравнения. Напомню следующую формулу:
a = logb ba
Разумеется, под выражением «любое число b», я подразумеваю такие числа, которые удовлетворяют требования, накладываемые на основание логарифма, т. е.
1 ≠ b > 0
Вот при таких b, а поскольку основание у нас уже известно, то это требование будет выполняться автоматически. Но при таких b — любых, которые удовлетворяют данное требование — данный переход может быть выполнен, и у нас получится каноническая форма, в которой можно избавиться от знака логарифма.
В процессе преобразования логарифмических уравнений может произойти неявное расширение области определения. Зачастую ученики этого даже не замечают, что приводит к ошибкам и неправильным ответам.
Начнем с простейших конструкций. Простейшим логарифмическим уравнением называется следующее:
logaf(x) = b
Обратите внимание: x присутствует лишь в одном аргументе одного логарифма. Как мы решаем такие уравнения? Используем каноническую форму. Для этого представляем число b = logaab, и наше уравнение перепишется в следующем виде:
logaf(x) = logaab
Данная запись называется канонической формой. Именно к ней следует сводить любое логарифмическое уравнение, которое вы встретите не только в сегодняшнем уроке, но и в любой самостоятельной и контрольной работе.
Как прийти к канонической форме, какие приемы использовать — это уже вопрос практики. Главное понимать: как только вы получите такую запись, можно считать, что задача решена. Потому что следующим шагом будет запись:
f(x) = ab
Другими словами, мы избавляемся от знака логарифма и просто приравниваем аргументы.
К чему весь этот разговор? Дело в том, что каноническая форма применима не только к простейшим задачам, но и к любым другим. В частности и к тем, которые мы будем решать сегодня. Давайте посмотрим.
Первая задача:

В чем проблема данного уравнения? В том, что функция стоит сразу в двух логарифмах. Задачу можно свести к простейшей, просто вычтя один логарифм из другого. Но возникают проблемы с областью определения: могут появиться лишние корни. Поэтому давайте просто перенесем один из логарифмов вправо:

Вот такая запись уже гораздо больше похожа на каноническую форму. Но есть еще один нюанс: в канонической форме аргументы должны быть одинаковы. А у нас слева стоит логарифм по основанию 3, а справа — по основанию 1/3. Знаит, нужно привести эти основания к одному и тому же числу. Например, вспомним, что такое отрицательные степени:
1/3 = 3−1
А затем воспользуемся вынесем показатель «−1» за пределы log в качестве множителя:

Обратите внимание: степень, которая стояла в основании, переворачивается и превращается в дробь. Мы получили почти каноническую запись, избавившись от разных оснований, но взамен получили множитель «−1» справа. Давайте внесем этот множитель в аргумент, превратив его в степень:

Разумеется, получив каноническую форму, мы смело зачеркиваем знак логарифма и приравниваем аргументы. При этом напомню, что при возведении в степень «−1» дробь просто переворачивается — получается пропорция.
Воспользуемся основным свойством пропорции и перемножим ее крест-накрест:
(x− 4) (2x− 1) = (x− 5) (3x− 4)
2x2 − x− 8x + 4 = 3x2 − 4x− 15x + 20
2x2 − 9x + 4 = 3x2 − 19x + 20
x2 − 10x + 16 = 0
Перед нами приведенное квадратное уравнение, поэтому решаем его с помощью формул Виета:
(x − 8)(x − 2) = 0
x1 = 8; x2 = 2
Вот и все. Думаете, уравнение решено? Нет! За такое решение мы получим 0 баллов, потому что в исходном уравнении присутствуют сразу два логарифма с переменной x. Поэтому требуется учесть область определения.
И здесь начинается самое веселое. Большинство учеников путаются: в чем состоит область определения логарифма? Разумеется, все аргументы (у нас их два) должны быть больше нуля:
(x− 4)/(3x− 4) > 0
(x− 5)/(2x− 1) > 0
Каждое из этих неравенств нужно решить, отметить на прямой, пересечь — и только потом посмотреть, какие корни лежат на пересечении.
Скажу честно: такой прием имеет право на существование, он надежный, и вы получите правильный ответ, однако в нем слишком много лишних действий. Поэтому давайте еще раз пройдемся по нашему решению и посмотрим: где именно требуется применить область определения? Другими словами, нужно четно понимать, когда именно возникают лишние корни.
Именно на последнем шаге происходит расширение области определения! Как только мы перешли к дробно-рациональному уравнению, избавившись от знаков log, требования к переменной xрезко поменялись!
Следовательно, область определения можно считать не в самом начале решения, а только на упомянутом шаге — перед непосредственным приравниваем аргументов.
Здесь-то и кроется возможность для оптимизации. С одной стороны, от нас требуется, чтобы оба аргумента были больше нуля. С другой — далее мы приравниваем эти аргументы. Следовательно, если хотя бы один и них будет положителен, то и второй тоже окажется положительным!
Вот и получается, что требовать выполнение сразу двух неравенств — это излишество. Достаточно рассмотреть лишь одну из этих дробей. Какую именно? Та, которая проще. Например, давайте разберемся с правой дробью:
(x− 5)/(2x− 1) > 0
Это типичное дробно-рациональное неравенство, решаем его методом интервалов:

Как расставить знаки? Возьмем число, заведомо большее всех наших корней. Например 1 млрд. И подставляем его дробь. Получим положительное число, т.е. справа от корня x = 5 будет стоять знак «плюс».
Затем знаки чередуются, потому что корней четной кратности нигде нет. Нас интересуют интервалы, где функция положительна. Следовательно, x∈ (−∞; −1/2)∪(5; +∞).
Теперь вспоминаем про ответы: x = 8 и x = 2. Строго говоря, это еще не ответы, а лишь кандидаты на ответ. Какой из них принадлежит указанному множеству? Конечно, x = 8. А вот x = 2 нас не устраивает по области определения.
Итого ответом к первому логарифмическому уравнению будет x = 8. Вот теперь мы получили грамотное, обоснованное решение с учетом области определения.
Переходим ко второму уравнению:
log5 (x − 9) = log0,5 4 − log5 (x − 5) + 3
Напоминаю, что если в уравнении присутствует десятичная дробь, то от нее следует избавиться. Другими словами, перепишем 0,5 в виде обычной дроби. Сразу замечаем, что логарифм, содержащий это основание, легко считается:

Это очень важны момент! Когда у нас и в основании, и в аргументе стоят степени, мы можем вынести показатели этих степеней по формуле:

Возвращаемся к нашему исходному логарифмическому уравнению и переписываем его:
log5 (x− 9) = 1 − log5 (x− 5)
Получили конструкцию, довольно близкую к канонической форме. Однако нас смущают слагаемые и знак «минус» справа от знака равенства. Давайте представим единицу как логарифм по основанию 5:
log5 (x − 9) = log5 51 − log5 (x − 5)
Вычтем логарифмы справа (при этом их аргументы делятся):
log5(x − 9) = log5 5/(x− 5)
Прекрасно. Вот мы и получили каноническую форму! Зачеркиваем знаки logи приравниваем аргументы:
(x − 9)/1 = 5/(x − 5)
Это пропорция, которая легко решается умножением крест-накрест:
(x − 9)(x − 5) = 51
x2 − 9x − 5x + 45 = 5
x2 − 14x + 40 = 0
Очевидно, перед нами приведенное квадратное уравнение. Оно легко решается с помощью формул Виета:
(x − 10)(x − 4) = 0
x1 = 10
x2 = 4
Мы получили два корня. Но это не окончательные ответы, а лишь кандидаты, потому что логарифмическое уравнение требует еще и проверки области определения.
Напоминаю: не надо искать, когда каждый из аргументов будет больше нуля. Достаточно потребовать, чтобы один аргумент — либо x − 9, либо 5/(x − 5) — был больше нуля. Рассмотрим первый аргумент:
x − 9 > 0
x > 9
Очевидно, что этому требованию удовлетворяет лишь x = 10. Это и есть окончательный ответ. Все задача решена.
Еще раз ключевые мысли сегодняшнего урока:
Разумеется, мы сами выбираем, из какого аргумента составлять неравенство, поэтому логично выбирать самый простой. Например, во втором уравнении мы выбрали аргумент (x − 9) —линейную функцию, в противовес дробно-рациональному второму аргументу. Согласитесь, решать неравенство x − 9 > 0 значительно проще, чем 5/(x − 5) > 0. Хотя результат получается один и тот же.
Данное замечание существенно упрощает поиск ОДЗ, но будьте внимательны: использовать одно неравенство вместо двух можно только том случае, когда аргументы именно приравниваются друг к другу!
Конечно, кто-то сейчас спросит: а что, бывает по-другому? Да, бывает. Например, в самом шаге, когда мы перемножаем два аргумента, содержащие переменную, заложена опасность возникновения лишних корней.
Судите сами: сначала требуется, чтобы каждый из аргументов был больше нуля, но после перемножения достаточно, чтобы их произведение было больше нуля. В результате упускается случай, когда каждая из этих дробей отрицательна.
Поэтому если вы только начинаете разбираться со сложными логарифмическими уравнениями, ни в коем случае не перемножайте логарифмы, содержащие переменную x — уж слишком часто это приведет к возникновению лишних корней. Лучше сделайте один лишний шаг, перенесите одно слагаемое в другую сторону составьте каноническую форму.
Ну, а как поступать в том случае, если без перемножения таких логарифмов не обойтись, мы обсудим в следующем видеоуроке.:)
Сегодня мы разберем довольно скользкую тему, касающуюся логарифмических уравнений, а точнее — вынесение степеней из аргументов и оснований логарифмов.
Я бы даже сказал, речь пойдет о вынесении четных степеней, потому что именно с четными степенями возникает большинство затруднений и при решении реальных логарифмических уравнений.
Начнем с канонической формы. Допустим, у нас есть уравнение вида logaf(x) = b. В этом случае мы переписываем число b по формуле b = logaab. Получается следующее:
logaf(x) = logaab
Затем мы приравниваем аргументы:
f(x) = ab
Канонической формой называется предпоследняя формула. Именно к ней стараются свести любое логарифмическое уравнение, каким бы сложным и страшным оно не казалось на первый взгляд.
Вот давайте и попробуем. Начнем с первой задачи:

Предварительное замечание: как я уже говорил, все десятичные дроби в логарифмическом уравнении лучше перевести ее в обычные:
0,001 = 1/1000
0,5 = 5/10 = 1/2
Перепишем наше уравнение с учетом этого факта. Заметим, что и 1/1000, и 100 являются степенью десятки, а затем вынесем степени отовсюду, где они есть: из аргументов и даже из основания логарифмов:

И вот здесь у многих учеников возникает вопрос: «Откуда справа взялся модуль?» Действительно, почему бы не написать просто (х − 1)? Безусловно, сейчас мы напишем (х − 1), но право на такую запись нам дает учет области определения. Ведь в другом логарифме уже стоит (х − 1), и это выражение должно быть больше нуля.
Но когда мы выносим квадрат из основания логарифма, мы обязаны оставить в основании именно модуль. Поясню почему.
Дело в том, что с точки зрения математики вынесение степени равносильно извлечению корня. В частности, когда из выражения (x− 1)2 выносится квадрат, мы по сути извлекаем корень второй степени. Но корень из квадрата — это не что иное как модуль. Именно модуль, потому что даже если выражение х − 1 будет отрицательным, при возведении в квадрат «минус» все равно сгорит. Дальнейшее извлечение корня даст нам положительное число — уже без всяких минусов.
В общем, чтобы не допускать обидных ошибок, запомните раз и навсегда:
Корень четной степени из любой функции, которая возведена в эту же степень, равен не самой функции, а ее модулю:
![]()
Возвращаемся к нашему логарифмическому уравнению. Говоря про модуль, я утверждал, что мы можем безболезненно снять его. Это правда. Сейчас объясню почему. Строго говоря, мы обязаны были рассмотреть два варианта:
Каждый из этих вариантов нужно было бы решить. Но есть одна загвоздка: в исходной формуле уже присутствует функция (х − 1) без всякого модуля. И следуя области определения логарифмов, мы вправе сразу записать, что х − 1 > 0.
Это требование должно выполняться независимо от всяких модулей и других преобразований, которые мы выполняем в процессе решения. Следовательно, второй вариант рассматривать бессмысленно — он никогда не возникнет. Даже если при решении этой ветки неравенства мы получим какие-то числа, они все равно не войдут в окончательный ответ.
В общем, можно считать, что |х − 1| = х − 1. Тогда наше уравнение перепишется в следующем виде:

Теперь мы буквально в одном шаге от канонической формы логарифмического уравнения. Давайте представим единицу в следующем виде:
1 = logx − 1 (x− 1)1
Кроме того, внесем множитель −4, стоящий справа, в аргумент:
logx − 1 10−4 = logx − 1 (x− 1)
Перед нами каноническая форма логарифмического уравнения. Избавляемся от знака логарифма:
10−4 = x− 1
Но поскольку в основании стояла функция (а не простое число), дополнительно потребуем, чтобы эта функция была больше нуля и не равна единице. Получится система:

Поскольку требование х − 1 > 0 выполняется автоматически (ведь х − 1 = 10−4), одно из неравенств можно вычеркнуть из нашей системы. Второе условие также можно вычеркнуть, потому что х − 1 = 0,0001 < 1. Итого получаем:
х = 1 + 0,0001 = 1,0001
Это единственный корень, который автоматически удовлетворяет всем требованиям области определения логарифма (впрочем, все требования были отсеяны как заведомо выполненные в условиях нашей задачи).
Итак, второе уравнение:
3 log3xx = 2 log9xx2
Чем это уравнение принципиально отличается от предыдущего? Уже хотя бы тем, что основания логарифмов — 3х и 9х — не являются натуральными степенями друг друга. Следовательно, переход, который мы использовали в предыдущем решении, невозможен.
Давайте хотя бы избавимся от степеней. В нашем случае единственная степень стоит во втором аргументе:
3 log3xx = 2 ∙ 2 log9x|x|
Впрочем, знак модуля можно убрать, ведь переменная х стоит еще и в основании, т.е. х > 0 ⇒ |х| = х. Перепишем наше логарифмическое уравнение:
3 log3xx = 4 log9xx
Получили логарифмы, в которых одинаковые аргументы, но разные основания. Как поступить дальше? Вариантов тут множество, но мы рассмотрим лишь два из них, которые наиболее логичны, а самое главное — это быстрые и понятные приемы для большинства учеников.
Первый вариант мы уже рассматривали: в любой непонятной ситуации переводите логарифмы с переменным основанием к какому-нибудь постоянному основанию. Например, к двойке. Формула перехода проста:

Разумеется, в роли переменной с должно выступать нормальное число: 1 ≠ c > 0. Пусть в нашем случае с = 2. Теперь перед нами обычное дробно-рациональное уравнение. Собираем все элементы слева:

Очевидно, что множитель log2x лучше вынести, поскольку он присутствует и в первой, и во второй дроби.
Дальше все просто. Произведение равно нулю, когда хотя бы один из множителей равен нулю:
log2x = 0;
х = 1;
3 log2 9х = 4 log2 3x
Разбиваем каждый log на два слагаемых:
log2 9х = log2 9 + log2 x = 2 log2 3 + log2 x;
log2 3x = log2 3 + log2x
Перепишем обе части равенства с учетом этих фактов:
3 (2 log2 3 + log2 x) = 4 (log2 3 + log2 x)
6 log2 3 + 3 log2 x = 4 log2 3 + 4 log2 x
2 log2 3 = log2x
Теперь осталось внести двойку под знак логарифма (она превратится в степень: 32 = 9):
log2 9 = log2x
Перед нами классическая каноническая форма, избавляемся от знака логарифма и получаем:
х = 9
Как и предполагалось, этот корень оказался больше нуля. Осталось проверить область определения. Посмотрим на основания:
3х ≠ 1
9х ≠ 1
Но корень x = 9 удовлетворяет этим требованиям. Следовательно, он является окончательным решением.
Вывод из данного решения просто: не пугайтесь длинных выкладок! Просто в самом начале мы выбрали новое основание наугад — и это существенно усложнило процесс.
Но тогда возникает вопрос: какое же основание является оптимальным? Об этом я расскажу во втором способе.
Давайте вернемся к нашему исходному уравнению:
3 log3x x = 2 log9x x2
3 log3x x = 2 ∙ 2 log9x |x|
х > 0 ⇒ |х| = х
3 log3xx = 4 log9xx
Теперь немного подумаем: какое число или функция будет оптимальным основанием? Очевидно, что лучшим вариантом будет с = х — то, что уже стоит в аргументах. В этом случае формула logab = logcb/logca примет вид:

Другими словами, выражение просто переворачивается. При этом аргумент и основание меняется местами.
Эта формула очень полезна и очень часто применяется при решении сложных логарифмических уравнений. Однако при использовании этой формулы возникает один очень серьезный подводный камень. Если вместо основания мы подставляем переменную х, то на нее накладываются ограничения, которых ранее не наблюдалось:
0 < х ≠ 1
Такого ограничения в исходном уравнении не было. Поэтому следует отдельно проверить случай, когда х = 1. Подставим это значение в наше уравнение:
3 log3 1 = 4 log9 1
0 = 0
Получаем верное числовое равенство. Следовательно, х = 1 является корнем. Точно такой же корень мы нашли в предыдущем методе в самом начале решения.
А вот теперь, когда мы отдельно рассмотрели этот частный случай, смело полагаем, что х ≠ 1. Тогда наше логарифмическое уравнение перепишется в следующем виде:
3 logx 9x = 4 logx 3x
Раскладываем оба логарифма по той же формуле, что и раньше. При этом заметим, что logxx = 1:
3 (logx 9 + logx x) = 4 (logx 3 + logx x)
3 logx 9 + 3 = 4 logx 3 + 4
3 logx 32 − 4 logx 3 = 4 − 3
2 logx 3 = 1
Вот мы и пришли к канонической форме:
logx 9 = logxx1
x = 9
Получили второй корень. Он удовлетворяет требованию х ≠ 1. Следовательно, х = 9 наравне с х = 1 является окончательным ответом.
Как видим, объем выкладок немножко сократился. Но при решении реального логарифмического уравнения количество действий будет намного меньше еще и потому, что от вас не требуется столь подробно расписывать каждый шаг.
Ключевое правило сегодняшнего урока состоит в следующем: если в задаче присутствует четная степень, из которой извлекают корень такой же степени, то на выходе мы получи модуль. Однако этот модуль можно убрать, если обратить внимание на область определения логарифмов.
Но будьте внимательны: большинство учеников после этого урока считают, что им все понятно. Но при решении реальных задач они не могут воспроизвести всю логическую цепочку. В результате уравнение обрастает лишними корнями, а ответ получается неправильным.
Поэтому обязательно практикуйтесь: скачивайте задачи для самостоятельной работы, решайте их и сравнивайте с ответами. А у меня на сегодня все.:)