Из предыдущего видео (см. «Простейшие логарифмические уравнения») мы узнали, как решается простейшее логарифмическое уравнение:
log a f (x) = b ⇒ log a f (x) = log a a b ⇒ f (x) = a b
Однако внимательные ученики уже наверняка заметили: в исходном логарифме присутствует ограничение на функцию f (x):
f (x) > 0
А в итоговой формуле никаких ограничений нет. Не значит ли это, что мы незаметно для себя расширим область определения и тем самым, возможно, наткнемся на лишние корни? Нет, не значит! Решая простейшие уравнения, вообще нет нужды учитывать область определения логарифма — все уже учтено во время преобразований. Взгляните, чему должна быть равна наша функция:
f (x) = a b
Число a обязательно будет положительным, поскольку это основание логарифма. А число b стоит в показателе, и каким бы оно ни было, конструкция a b всегда будет положительной. Таким образом, все ограничения, накладываемые исходным уравнением, выполняются автоматически.
Совсем другое дело — сама функция, которая стоит под знаком логарифма. Вот с ней надо работать аккуратно, потому что там могут стоять весьма суровые конструкции. Взгляните на примеры:
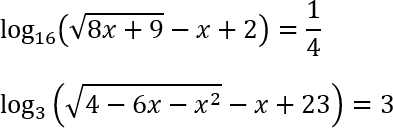
Оба этих уравнения будут подробно разобраны в сегодняшнем видеоуроке.