Сегодня мы вернемся к решению неравенств методом интервалов, однако рассмотрим не обычные неравенства (где просто перемножаются скобки), а нестандартные, в которых присутствуют корни.
Итак, первая задача:
Задача 1. Решите неравенство:
![]()
В чем особенность такого неравенства? Какие ограничения для нас вносит наличие радикала? Все очень просто. Согласно определению, арифметический квадратный корень из любой функции f (x) всегда неотрицателен, т.е. больше или равен нуля.
А это значит, что мы можем без всяких затруднений избавиться от корня, просто зачеркнув его. Но при условии, что это выражение отлично от нуля. Потому что, напомню:
Основное свойство неравенства: обе части неравенства можно умножать и делить на любое число, отличное от нуля.
Таким образом, случай, когда корень (а значит — и подкоренное выражение) равняется нулю, следует проверять отдельно. Имеем:
15 − 5x = 0;
15 = 5x;
x = 3.
Подставим найденное число в исходное неравенство — получим:
(3 − 5) ∙ 0 < 0;
0 < 0.
Последнее неравенство, очевидно, является полным бредом. Следовательно, x = 3 не является решением исходного неравенства. А это значит, что мы можем спокойно разделить все неравенство на корень. Получим:
x − 8 < 0
x < 8
Однако если мы просто запишем такой ответ — (−∞; 8) — то, как вы уже поняли, это будет неправильным решением. Все дело в том, что, избавляясь от корня в исходном неравенстве, мы одновременно расширяем область определения.
Судите сами: в неравенстве x < 0 переменная x может принимать абсолютно любые значения, потому что линейная функция определена на всей числовой прямой. А вот в исходном неравенстве подкоренное выражение должно быть неотрицательным, потому что корень из отрицательного числа не определен.
Поэтому возникает еще одно требование:
15 − 5x ≥ 0
15 ≥ 5x
x ≤ 3
Обратите внимание знак «больше или равно» никак не связан с тем, что стояло в исходном неравенстве — это просто требование области определения корня.
При решении неравенств, содержащих корни, подкоренная функция должна быть неотрицательной в любом случае — независимо от знака исходного неравенства.
Теперь отметим наши требования на двух параллельных прямых:
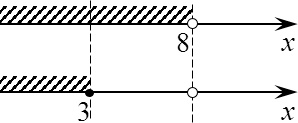
Итак, с одной стороны, x должен быть меньше 8 (т.е. левее восьмерки). С другой — не больше 3 (опять же левее). Пересекаем наши множества и получаем интервал:
x ∈ (−∞; 3]
Но и это не является окончательным и правильным ответом! Дело в том, что в самом начале решения мы убедились, что x = 3 нас не устраивает. Следовательно, эту точку надо выколоть. Поэтому окончательным ответом будет множество:
x ∈ (−∞; 3)
Итак, переходим ко второму неравенству.
Задача 2. Решите неравенство:
![]()
Выполняем все те же самые действия, как и в прошлый раз. Для начала проверяем: является ли ответом тот случай, когда подкоренное выражение равно нулю.
16 − x2 = 0
x2 = 16
x = ± 4
Подставляем полученные числа в исходное неравенство и получаем:
(16 − 9) ∙ 0 > 0
0 > 0
Очевидно, мы вновь получили неверное неравенство (ноль больше нуля — полный бред). А это значит, что корни x = 4 и x = −4 не являются решением. Эти точки нужно будет выколоть.
С учетом данного факта нужно просто выполоть эти точки и решить обычное неравенство:
x2 − 9 > 0
(x − 3)(x + 3) > 0
Чертим прямую, отмечаем нули выражения, стоящего справа — получаем:
![]()
Поскольку нас интересуют положительные области, отмечаем интервалы по бокам.
С другой стороны, в исходном неравенстве у нас есть корень. Поэтому нельзя забывать про определение:
16 − x2 ≥ 0
x2 ≤ 4
−4 < x < 4
Осталось начертить на двух параллельных прямых полученные множества:
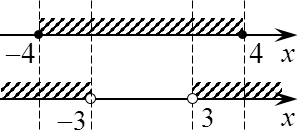
Пересекаем заштрихованные области (потому что указанные требования должны выполняться одновременно). Кроме того, вспоминаем, что значения x = ±4 нас не устраивают. Следовательно, эти точки нужно выколоть из итогового ответа. Получим:
x ∈ (−4; −3) ∪ (3; 4)
Вот такому множеству должно принадлежать число x, чтобы выполнялось исходное неравенство. Все точки при этом выколоты. Все, задача решена.
Надеюсь, этот урок поможет вам не запутаться при решении задач, содержащих корни. Тренируйтесь в решении неравенство методом интервалов — и до новых встреч.