Метод интервалов: случай нестрогих неравенств

15 ноября 2012

Сегодня мы узнаем, как использовать метод интервалов для решения нестрогих неравенств. Во многих учебниках нестрогие неравенства определяются следующим образом:

Нестрогое неравенство — это неравенство вида f (x) ≥ 0 или f (x) ≤ 0, которое равносильно совокупности строгого неравенства и уравнения: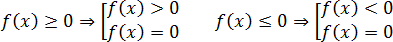

В переводе на русский язык это значит, что нестрогое неравенство f (x) ≥ 0 — это объединение классического уравнения f (x) = 0 и строгого неравенства f (x) > 0. Другими словами, теперь нас интересуют не только положительные и отрицательные области на прямой, но и точки, где функция равна нулю.

Отрезки и интервалы: в чем разница?

Прежде чем решать нестрогие неравенства, давайте вспомним, чем интервал отличается от отрезка:

Интервал — это часть прямой, ограниченная двумя точками. Но эти точки не принадлежат интервалу. Интервал обозначается круглыми скобками: (1; 5), (−7; 3), (11; 25) и т.д.;
Отрезок — это тоже часть прямой, ограниченная двумя точками. Однако эти точки тоже являются частью отрезка. Отрезки обозначаются квадратными скобками: [1; 5], [−7; 3], [11; 25] и т.д.

Чтобы не путать интервалы с отрезками, для них разработаны специальные обозначения: интервал всегда обозначается выколотыми точками, а отрезок — закрашенными. Например:

На этом рисунке отмечен отрезок [2; 5] и интервал (9; 11). Обратите внимание: концы отрезка отмечены закрашенными точками, а сам отрезок обозначается квадратными скобками. С интервалом все иначе: его концы выколоты, а скобки — круглые.

Метод интервалов для нестрогих неравенств

К чему была вся эта лирика про отрезки и интервалы? Очень просто: для решения нестрогих неравенств все интервалы заменяются отрезками — и получится ответ. По существу, мы просто добавляем к ответу, полученному методом интервалов, границы этих самых интервалов. Сравните два неравенства:

Задача. Решите строгое неравенство:

(x − 5)(x + 3) > 0

Решаем методом интервалов. Приравниваем левую часть неравенства к нулю:

(x − 5)(x + 3) = 0;
x − 5 = 0 ⇒ x = 5;
x + 3 = 0 ⇒ x = −3;

Отмечаем полученные корни на координатной оси:

Справа стоит знак плюс. В этом легко в этом убедиться, подставив миллиард в функцию:

f (x) = (x − 5)(x + 3)

Осталось выписать ответ. Поскольку нас интересуют положительные интервалы, имеем:

x ∈ (−∞; −3) ∪ (5; +∞)

Задача. Решите нестрогое неравенство:

(x − 5)(x + 3) ≥ 0

Начало такое же, как и для строгих неравенств: работает метод интервалов. Приравниваем левую часть неравенства к нулю:

(x − 5)(x + 3) = 0;
x − 5 = 0 ⇒ x = 5;
x + 3 = 0 ⇒ x = −3;

Отмечаем полученные корни на координатной оси:

В предыдущей задаче мы уже выяснили, что справа стоит знак плюс. Напомню, в этом легко убедиться, подставив миллиард в функцию:

f (x) = (x − 5)(x + 3)

Осталось записать ответ. Поскольку неравенство нестрогое, а нас интересуют положительные значения, имеем:

x ∈ (−∞; −3] ∪ [5; +∞)

Итак, основное отличие строгих и нестрогих неравенств:

В строгих неравенствах нас не интересуют концы отрезка, поэтому они отмечаются выколотыми точками. Такие точки никогда не входят в ответ, о чем говорят круглые скобки на первом ответе: x ∈ (−∞; −3) ∪ (5; +∞);
И наоборот, в нестрогих неравенствах концы отрезка входят в ответ. На графике они отмечаются закрашенными точками, а в ответе указываются квадратными скобками: x ∈ (−∞; −3] ∪ [5; +∞).

Вот и вся разница! Просто запомните: в строгих неравенствах точки выколоты, а в нестрогих — закрашены.

Почему бесконечности всегда стоят в круглых скобках

У внимательного читателя наверняка возник вопрос: почему бесконечности отмечаются круглыми скобками даже в нестрогих неравенствах? Например, почему в последней задаче мы пишем не [−∞; −3] ∪ [5; +∞], а (−∞; −3] ∪ [5; +∞)?

Что ж, это не опечатка. Бесконечность действительно обозначается круглой скобкой, даже если неравенство — нестрогое. Чтобы понять, почему так происходит, достаточно вспомнить определение бесконечности.

Бесконечность — это гипотетическое число, которое больше любого другого числа, участвующего в решении.

Трудность заключается в том, что нельзя работать с бесконечностью напрямую. Мы можем лишь приблизиться к ней, подставляя такие зверские числа, как 1 000 000 и даже 1 000 000 000. Но добраться до самой бесконечности все равно нельзя.

Именно поэтому бесконечность обозначают круглыми скобками. Ведь хотя бесконечность и ограничивает всю числовую прямую, сама она не принадлежит этой прямой.

Ситуация точь-в-точь такая же, как с границами интервалов. Рассмотрим все числа из интервала:

x ∈ (0; 1)

Эта запись означает, что число x = 0 не принадлежит интервалу, однако любое число, которое больше нуля и меньше единицы — принадлежит. В частности, этому интервалу принадлежат следующие числа:

Попробуем отметить эти числа на координатной прямой. Поскольку каждое следующее число вдвое меньше предыдущего, нам придется несколько раз менять масштаб. Получим что-то вроде этого:

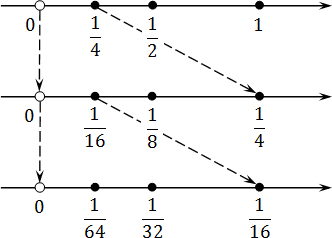
как отметить маленькие числа на координатной прямой

Что дает нам этот график? Оказывается, при достаточно крупном масштабе можно отметить любое число, сколь угодно близкое к нулю. При этом сам ноль никуда не денется — он остается недостижимой границей. Именно это и подразумевается, когда речь заходит о концах интервала.

То же самое происходит и с бесконечностью. Разница лишь в том, что масштаб надо не увеличивать, а уменьшать:

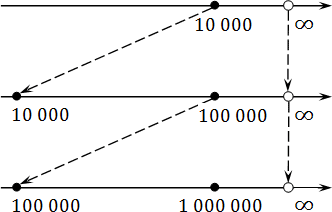
как отметить большие числа на координатной прямой

Мы можем сколь угодно долго идти к бесконечности, но так и не достигнем ее. Вот почему бесконечности обозначают круглыми скобками, подобно границам интервала.

Примеры решения неравенств

В заключение кратко разберем два нестрогих неравенства. И если в первой задаче еще есть какие-то пояснения, то вторая задача будет оформлена именно так, как и надо оформлять настоящее решение.

Задача. Решите неравенство:

(x + 8)(x − 3) ≤ 0

Как обычно, приравниваем все к нулю:

(x + 8)(x − 3) = 0;
x + 8 = 0 ⇒ x = −8;
x − 3 = 0 ⇒ x = 3.

Теперь рассматриваем функцию, которая находится в левой части неравенства:

f (x) = (x + 8)(x − 3)

Подставим в эту функцию бесконечность — получим выражение вида:

(+) · (+) = (+)

Чертим координатную ось, отмечаем корни и расставляем знаки:

Поскольку мы решаем неравенство (x + 8)(x − 3) ≤ 0 или, что то же самое, f (x) ≤ 0, осталось записать ответ:

x ∈ [−8; 3]

Задача. Решите неравенство:

x(12 − 2x)(3x + 9) ≥ 0

x(12 − 2x)(3x + 9) = 0;
x = 0;
12 − 2x = 0 ⇒ 2x = 12 ⇒ x = 6;
3x + 9 = 0 ⇒ 3x = −9 ⇒ x = −3.

x ≥ 6 ⇒ f (x) = x(12 − 2x)(3x + 9) → (+) · (−) · (+) = (−) < 0;
x ∈ (−∞ −3] ∪ [0; 6].

Смотрите также: