Иррациональные неравенства. Часть 1

6 марта 2012

Всякое неравенство, в состав которого входит функция, стоящая под корнем, называется иррациональным. Существует два типа таких неравенств:

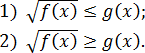
В первом случае корень меньше функции g(x), во втором — больше. Если g(x) — константа, неравенство резко упрощается. Обратите внимание: внешне эти неравенства очень похожи, но схемы решения у них принципиально различаются.

Сегодня научимся решать иррациональные неравенства первого типа — они самые простые и понятные. Знак неравенства может быть строгим или нестрогим. Для них верно следующее утверждение:

Теорема. Всякое иррациональное неравенство вида

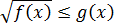
Равносильно системе неравенств:

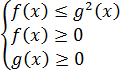
Неслабо? Давайте рассмотрим, откуда берется такая система:

1. f (x) ≤ g² (x) — тут все понятно. Это исходное неравенство, возведенное в квадрат;
2. f (x) ≥ 0 — это ОДЗ корня. Напомню: арифметический квадратный корень существует только из неотрицательного числа;
3. g(x) ≥ 0 — это область значений корня. Возводя неравенство в квадрат, мы сжигаем минусы. В результате могут возникнуть лишние корни. Неравенство g(x) ≥ 0 отсекает их.

Многие ученики «зацикливаются» на первом неравенстве системы: f (x) ≤ g² (x) — и напрочь забывают два других. Результат предсказуем: неправильное решение, потерянные баллы.

Поскольку иррациональные неравенства — достаточно сложная тема, разберем сразу 4 примера. От элементарных до действительно сложных. Все задачи взяты из вступительных экзаменов МГУ им. М. В. Ломоносова.

Примеры решения задач

Задача. Решите неравенство:

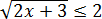
Перед нами классическое иррациональное неравенство: f (x) = 2x + 3; g(x) = 2 — константа. Имеем:

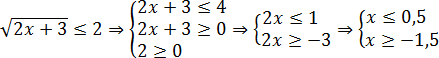
Из трех неравенств к концу решения осталось только два. Потому что неравенство 2 ≥ 0 выполняется всегда. Пересечем оставшиеся неравенства:

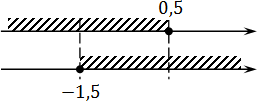
Итак, x ∈ [−1,5; 0,5]. Все точки закрашены, поскольку неравенства нестрогие.

Задача. Решите неравенство:

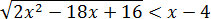
Применяем теорему:

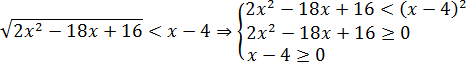
Решаем первое неравенство. Для этого раскроем квадрат разности. Имеем:

2x² − 18x + 16 < (x − 4)²;
2x² − 18x + 16 < x² − 8x + 16:
x² − 10x < 0;
x(x − 10) < 0;
x ∈ (0; 10).

Теперь решим второе неравенство. Там тоже квадратный трехчлен:

2x² − 18x + 16 ≥ 0;
x² − 9x + 8 ≥ 0;
(x − 8)(x − 1) ≥ 0;
x ∈ (−∞; 1]∪[8; +∞).

Наконец, решаем третье неравенство. Оно совсем простое:

x − 4 ≥ 0;
x ≥ 4;
x ∈ [4; +∞).

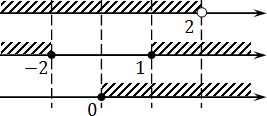
Осталось пересечь полученные множества. Отметим их на координатных прямых:

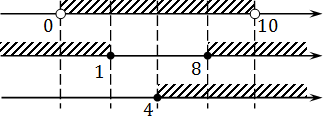
Поскольку мы решаем систему неравенств, выбираем отрезки, которые одновременно заштрихованы на всех трех осях.

Задача. Решите неравенство:

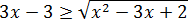
Сначала немного перепишем исходное неравенство:

Теперь применяем теорему:

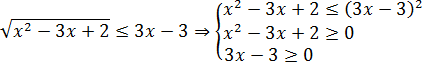
Все неравенства нестрогие. Решаем отдельно первое из них:

x² − 3x + 2 ≤ (3x − 3)²;
...
x ∈ (−∞; 7/8]∪[1; +∞).

Затем — второе:

x² − 3x + 2 ≥ 0;
(x − 2)(x − 1) ≥ 0;
x ∈ (−∞; 1]∪[2; +∞).

Наконец, последнее неравенство. Оно совсем легкое:

3x − 3 ≥ 0;
x ≥ 1;
x ∈ [1; +∞).

Пересекаем найденные множества и получаем ответ:

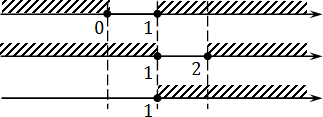
Обратите внимание: на пересечении возникает изолированная точка x = 1. В каждом множестве она является концом отрезка.

Задача. Решите неравенство:

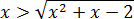
Перепишем иррациональное неравенство, а затем работаем по теореме:

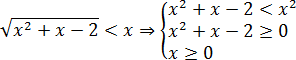
Первое неравенство сводится к линейному:

x² + x − 2 < x²;
x − 2 < 0;
x < 2;
x ∈ (−∞; 2).

Второе — классическое квадратное неравенство:

x² + x − 2 ≥ 0;
(x + 2)(x − 1) ≥ 0;
x ∈ (−∞; −2]∪[1; +∞).

Последнее неравенство — тоже линейное:

x ≥ 0;
x ∈ [0; +∞).

Отмечаем эти множества на координатных прямых и пересекаем:

1. Иррациональные неравенства. Часть 2
2. Особенности решения неравенств с радикалами
3. Правила комбинаторики в задаче B6
4. 4 совета: как избежать глупых ошибок на ЕГЭ по математике
5. Координаты вершин правильного тетраэдра
6. Задача B4 про два типа фундамента