На прошлом уроке мы научились складывать и вычитать десятичные дроби (см. урок «Сложение и вычитание десятичных дробей»). Заодно оценили, насколько упрощаются вычисления по сравнению с обычными «двухэтажными» дробями.
К сожалению, с умножением и делением десятичных дробей подобного эффекта не возникает. В некоторых случаях десятичная запись числа даже усложняет эти операции.
Для начала введем новое определение. Мы будем встречаться с ним довольно часто, и не только на этом уроке.
Значащая часть числа — это все, что находится между первой и последней ненулевой цифрой, включая концы. Речь идет только о цифрах, десятичная точка не учитывается.
Цифры, входящие в значащую часть числа, называются значащими цифрами. Они могут повторяться и даже быть равными нулю.
Например, рассмотрим несколько десятичных дробей и выпишем соответствующие им значащие части:
Обратите внимание: нули, стоящие внутри значащей части числа, никуда не деваются. Мы уже сталкивались с чем-то подобным, когда учились переводить десятичные дроби в обычные (см. урок «Десятичные дроби»).
Этот момент настолько важен, а ошибки здесь допускают так часто, что в ближайшее время я опубликую тест на эту тему. Обязательно потренируйтесь! А мы, вооружившись понятием значащей части, приступим, собственно, к теме урока.
Операция умножения состоит из трех последовательных шагов:
Еще раз напомню, что нули, стоящие по бокам от значащей части, никогда не учитываются. Игнорирование этого правила приводит к ошибкам.
Задача. Найдите значение выражения:
- 0,28 · 12,5;
- 6,3 · 1,08;
- 132,5 · 0,0034;
- 0,0108 · 1600,5;
- 5,25 · 10 000.
Работаем с первым выражением: 0,28 · 12,5.
Теперь разберемся с выражением 6,3 · 1,08.
Добрались до третьего выражения: 132,5 · 0,0034.
Следующее выражение: 0,0108 · 1600,5.
Наконец, последнее выражение: 5,25 · 10 000.
Обратите внимание на последний пример: поскольку десятичная точка перемещается в разных направлениях, суммарный сдвиг находится через разность. Это очень важный момент! Вот еще пример:
Рассмотрим числа 1,5 и 12 500. Имеем: 1,5 → 15 (сдвиг на 1 вправо); 12 500 → 125 (сдвиг на 2 влево). Мы «шагаем» на 1 разряд вправо, а затем — на 2 влево. В итоге, мы шагнули на 2 − 1 = 1 разряд влево.
Деление — это, пожалуй, самая сложная операция. Конечно, здесь можно действовать по аналогии с умножением: делить значащие части, а затем «двигать» десятичную точку. Но в этом случае возникает много тонкостей, которые сводят на нет потенциальную экономию.
Поэтому давайте рассмотрим универсальный алгоритм, который чуть-чуть длиннее, но намного надежнее:
Задача. Найдите значение выражения:
- 3,51 : 3,9;
- 1,47 : 2,1;
- 6,4 : 25,6:
- 0,0425 : 2,5;
- 0,25 : 0,002.
Считаем первое выражение. Для начала переведем оби дроби в десятичные:
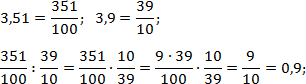
Аналогично поступим со вторым выражением. Числитель первой дроби снова разложится на множители:
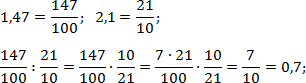
В третьем и четвертом примерах есть важный момент: после избавления от десятичной записи возникают сократимые дроби. Однако мы не будем выполнять это сокращение.
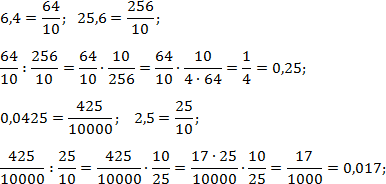
Последний пример интересен тем, что в числителе второй дроби стоит простое число. Здесь просто нечего разлагать на множители, поэтому считаем «напролом»:
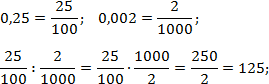
Иногда в результате деления получается целое число (это я про последний пример). В таком случае третий шаг вообще не выполняется.
Кроме того, при делении часто возникают «некрасивые» дроби, которые нельзя перевести в десятичные. Этим деление отличается от умножения, где результаты всегда представимы в десятичной форме. Разумеется, в таком случае последний шаг опять же не выполняется.
Обратите также внимание на 3-й и 4-й примеры. В них мы намеренно не сокращаем обычные дроби, полученные из десятичных. Иначе это усложнит обратную задачу — представление конечного ответа снова в десятичном виде.
Запомните: основное свойство дроби (как и любое другое правило в математике) само по себе еще не означает, что его надо применять везде и всегда, при каждом удобном случае.