Чтобы найти сумму или разность двух чисел, записанных в десятичной форме, надо выполнить три шага:
Как видите, сложение десятичных дробей почти ничем не отличается от сложения обычных чисел. Самое сложное — правильно сопоставить разряды слагаемых, чтобы десятичные точки находились на вертикальной прямой, друг под другом.
Задача. Найдите значение выражений:
8,125 + 17,4; 3,5 + 121,048.
Для каждого выражения приведем правильную запись и две неправильные (самые распространенные). Сначала — правильные:
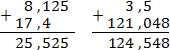
Теперь рассмотрим неправильные решения. В первом случае все числа «прижаты» к левому краю, во втором — к правому. Ответы получатся совсем другие:
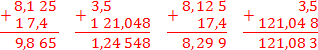
Как видите, ничего общего с тем, что должно получиться на самом деле.
Если в одном из слагаемых нет десятичной точки, ее ставят справа от всего числа. Например, возьмем числа 5,83 и 72. В этом случае операция сложения будет выглядеть так:
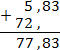
Кто-то скажет, что все эти отступы, сдвиги и запятые — ненужные сложности, и лучше работать «по старинке». Что ж, я никого не собираюсь переубеждать. Отмечу лишь, что новая технология всегда требуют более высокой квалификации от тех, кто собирается ее использовать. В этом плане десятичные дроби — следующий уровень развития после обычных.
Задача. Найдите значение выражений:
7,34 + 18,5; 13 + 0,25; 11,3 − 4,128; 5,21 − 11.
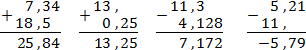
Эти примеры показывают, насколько упрощаются вычисления, когда дроби записаны в десятичной форме. Никаких дополнительных множителей, никаких общих знаменателей.
Чтобы почувствовать разницу, решим ту же задачу традиционным методом. Для этого переведем все десятичные дроби в обычные. Взгляните:
Задача. Найдите значение выражений:
7,34 + 18,5; 13 + 0,25; 11,3 − 4,128; 5,21 − 11.
Итак, переводим все десятичные дроби в обычные и считаем по классической схеме:
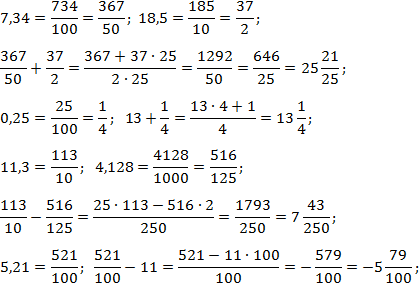
Мы специально не стали выполнять обратный переход — от обычной дроби к десятичной — чтобы немного сократить вычисления.
Видно, что длина решения выросла многократно. Поэтому старайтесь работать с десятичными дробями везде, где это возможно.