Сравнение дробей

2 сентября 2011

В этом уроке мы научимся сравнивать дроби между собой. Это очень полезный навык, который необходим для решения целого класса более сложных задач.

Для начала напомню определение равенства дробей:

Дроби a/b и c/d называются равными, если ad = bc.

Примеры:

1. 5/8 = 15/24, поскольку 5 · 24 = 8 · 15 = 120;
2. 3/2 = 27/18, поскольку 3 · 18 = 2 · 27 = 54.

Во всех остальных случаях дроби являются неравными, и для них справедливо одно из следующих утверждений:

1. Дробь a/b больше, чем дробь c/d;
2. Дробь a/b меньше, чем дробь c/d.

Дробь a/b называется большей, чем дробь c/d, если a/b − c/d > 0.

Дробь x/y называется меньшей, чем дробь s/t, если x/y − s/t < 0.

Обозначение:

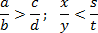
Примеры:

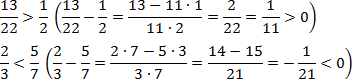
Таким образом, сравнение дробей сводится к их вычитанию. Вопрос: как не запутаться с обозначениями «больше» (>) и «меньше» (<)? Для ответа просто приглядитесь к тому, как выглядят эти знаки:

1. Расширяющаяся часть галки всегда направлена к большему числу;
2. Острый нос галки всегда указывает на меньшее число.

Часто в задачах, где требуется сравнить числа, между ними ставят знак «∨». Это — галка носом вниз, что как бы намекает: большее из чисел пока не определено.

Задача. Сравнить числа:

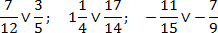
Следуя определению, вычтем дроби друг из друга:

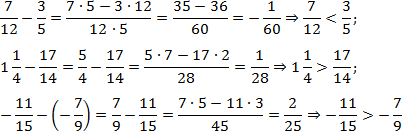
В каждом сравнении нам потребовалось приводить дроби к общему знаменателю. В частности, используя метод «крест-накрест» и поиск наименьшего общего кратного. Я намеренно не акцентировал внимание на этих моментах, но если что-то непонятно, загляните в урок «Сложение и вычитание дробей» — он совсем легкий.

Сравнение десятичных дробей

В случае с десятичными дробями все намного проще. Здесь не надо ничего вычитать — достаточно просто сравнить разряды. Не лишним будет вспомнить, что такое значащая часть числа. Тем, кто забыл, предлагаю повторить урок «Умножение и деление десятичных дробей» — это также займет буквально пару минут.

Положительная десятичная дробь X больше положительной десятичной дроби Y, если в ней найдется такой десятичный разряд, что:

1. Цифра, стоящая в этом разряде в дроби X, больше соответствующей цифры в дроби Y;
2. Все разряды старше данного у дробей X и Y совпадают.

Примеры:

1. 12,25 > 12,16. Первые два разряда совпадают (12 = 12), а третий — больше (2 > 1);
2. 0,00697 < 0,01. Первые два разряда опять совпадают (00 = 00), а третий — меньше (0 < 1).

Другими словами, мы последовательно просматриваем десятичные разряды и ищем различие. При этом большей цифре соответствует и большая дробь.

Однако это определение требует пояснения. Например, как записывать и сравнивать разряды до десятичной точки? Вспомните: к любому числу, записанному в десятичной форме, можно приписывать слева любое количество нулей. Вот еще пара примеров:

1. 0,12 < 951, т.к. 0,12 = 000,12 — приписали два нуля слева. Очевидно, 0 < 9 (речь идет о старшем разряде).
2. 2300,5 > 0,0025, т.к. 0,0025 = 0000,0025 — приписали три нуля слева. Теперь видно, что различие начинается в первом же разряде: 2 > 0.

Конечно, в приведенных примерах с нулями был явный перебор, но смысл именно такой: заполнить недостающие разряды слева, а затем сравнить.

Задача. Сравните дроби:

1. 0,029 ∨ 0,007;
2. 14,045 ∨ 15,5;
3. 0,00003 ∨ 0,0000099;
4. 1700,1 ∨ 0,99501.

По определению имеем:

1. 0,029 > 0,007. Первые два разряда совпадают (00 = 00), дальше начинается различие (2 > 0);
2. 14,045 < 15,5. Различие — во втором разряде: 4 < 5;
3. 0,00003 > 0,0000099. Здесь надо внимательно считать нули. Первые 5 разрядов в обеих дробях нулевые, но дальше в первой дроби стоит 3, а во второй — 0. Очевидно, 3 > 0;
4. 1700,1 > 0,99501. Перепишем вторую дробь в виде 0000,99501, добавив 3 нуля слева. Теперь все очевидно: 1 > 0 — различие обнаружено в первом же разряде.

К сожалению, приведенная схема сравнения десятичных дробей не универсальна. Этим методом можно сравнивать только положительные числа. В общем же случае алгоритм работы следующий:

1. Положительная дробь всегда больше отрицательной;
2. Две положительные дроби сравниваются по приведенному выше алгоритму;
3. Две отрицательные дроби сравниваются так же, но в конце знак неравенства меняется на противоположный.

Ну как, неслабо? Сейчас рассмотрим конкретные примеры — и все станет понятно.

Задача. Сравните дроби:

1. 0,0027 ∨ 0,0072;
2. −0,192 ∨ −0,39;
3. 0,15 ∨ −11,3;
4. 19,032 ∨ 0,0919295;
5. −750 ∨ −1,45.

1. 0,0027 < 0,0072. Здесь все стандартно: две положительные дроби, различие начинается на 4 разряде (2 < 7);
2. −0,192 > −0,39. Дроби отрицательные, 2 разряд разный. 1 < 3, но в силу отрицательности знак неравенства меняется на противоположный;
3. 0,15 > −11,3. Положительное число всегда больше отрицательного;
4. 19,032 > 0,091. Достаточно вторую дробь переписать в виде 00,091, чтобы увидеть, что различие возникает уже в 1 разряде;
5. −750 < −1,45. Если сравнить числа 750 и 1,45 (без минусов), легко видеть, что 750 > 001,45. Различие — в первом же разряде.

1. Перевод десятичной дроби в обычную
2. Периодические десятичные дроби
3. Комбинаторика в задаче B6: легкий тест
4. Площади многоугольников на координатной сетке
5. Четырехугольная пирамида: как найти координаты вершин
6. Задача B4: обмен валют в трех различных банках