Периодические десятичные дроби

9 февраля 2012

Помните, как в самом первом уроке про десятичные дроби я говорил, что существуют числовые дроби, не представимые в виде десятичных (см. урок «Десятичные дроби»)? Мы еще учились раскладывать знаменатели дробей на множители, чтобы проверить, нет ли там чисел, отличных от 2 и 5.

Так вот: я наврал. И сегодня мы научимся переводить абсолютно любую числовую дробь в десятичную. Заодно познакомимся с целым классом дробей с бесконечной значащей частью.

Периодическая десятичная дробь — это любая десятичная дробь, у которой:

Значащая часть состоит из бесконечного количества цифр;

Через определенные интервалы цифры в значащей части повторяются.

Набор повторяющихся цифр, из которых состоит значащая часть, называется периодической частью дроби, а количество цифр в этом наборе — периодом дроби. Остальной отрезок значащей части, который не повторяется, называется непериодической частью.

Поскольку определений много, стоит подробно рассмотреть несколько таких дробей:

Эта дробь встречается в задачах чаще всего. Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.

Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.

Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.

Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6. Для удобства повторяющиеся части отделены друг от друга пробелом — в настоящем решении так делать не обязательно.

Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.

Как видите, определение периодической дроби основано на понятии значащей части числа. Поэтому если вы забыли что это такое, рекомендую повторить — см. урок «Умножение и деление десятичных дробей».

Переход к периодической десятичной дроби

Рассмотрим обыкновенную дробь вида a/b. Разложим ее знаменатель на простые множители. Возможны два варианта:

В разложении присутствуют только множители 2 и 5. Эти дроби легко приводятся к десятичным — см. урок «Десятичные дроби». Такие нас не интересуют;
В разложении присутствует что-то еще, кроме 2 и 5. В этом случае дробь непредставима в виде десятичной, зато из нее можно сделать периодическую десятичную дробь.

Чтобы задать периодическую десятичную дробь, надо найти ее периодическую и непериодическую часть. Как? Переведите дробь в неправильную, а затем разделите числитель на знаменатель «уголком».

При этом будет происходить следующее:

Сначала разделится целая часть, если она есть;
Возможно, будет несколько чисел после десятичной точки;
Через некоторое время цифры начнут повторяться.

Вот и все! Повторяющиеся цифры после десятичной точки обозначаем периодической частью, а то, что стоит спереди — непериодической.

Задача. Переведите обыкновенные дроби в периодические десятичные:

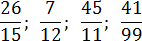
Все дроби без целой части, поэтому просто делим числитель на знаменатель «уголком»:

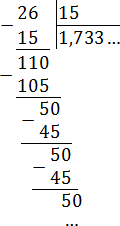
Как видим, остатки повторяются. Запишем дробь в «правильном» виде: 1,733 ... = 1,7(3).

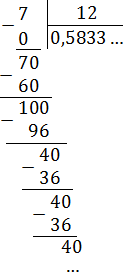
В итоге получается дробь: 0,5833 ... = 0,58(3).

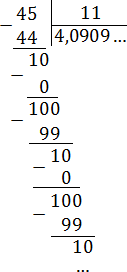
Записываем в нормальном виде: 4,0909 ... = 4,(09).

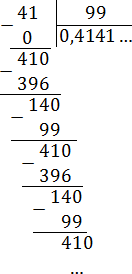
Получаем дробь: 0,4141 ... = 0,(41).

Переход от периодической десятичной дроби к обыкновенной

Рассмотрим периодическую десятичную дробь X = abc(a₁b₁c₁). Требуется перевести ее в классическую «двухэтажную». Для этого выполним четыре простых шага:

Найдите период дроби, т.е. подсчитайте, сколько цифр находится в периодической части. Пусть это будет число k;
Найдите значение выражения X · 10^k. Это равносильно сдвигу десятичной точки на полный период вправо — см. урок «Умножение и деление десятичных дробей»;
Из полученного числа надо вычесть исходное выражение. При этом периодическая часть «сжигается», и остается обычная дробь;
В полученном уравнении найти X. Все десятичные дроби переводим в обыкновенные.

Задача. Приведите к обыкновенной неправильной дроби числа:

9,(6);
32,(39);
0,30(5);
0,(2475).

Работаем с первой дробью: X = 9,(6) = 9,666 ...

В скобках содержится лишь одна цифра, поэтому период k = 1. Далее умножаем эту дробь на 10^k = 10¹ = 10. Имеем:

10X = 10 · 9,6666 ... = 96,666 ...

Вычитаем исходную дробь и решаем уравнение:

10X − X = 96,666 ... − 9,666 ... = 96 − 9 = 87;
9X = 87;
X = 87/9 = 29/3.

Теперь разберемся со второй дробью. Итак, X = 32,(39) = 32,393939 ...

Период k = 2, поэтому умножаем все на 10^k = 10² = 100:

100X = 100 · 32,393939 ... = 3239,3939 ...

Снова вычитаем исходную дробь и решаем уравнение:

100X − X = 3239,3939 ... − 32,3939 ... = 3239 − 32 = 3207;
99X = 3207;
X = 3207/99 = 1069/33.

Приступаем к третьей дроби: X = 0,30(5) = 0,30555 ... Схема та же самая, поэтому я просто приведу выкладки:

Период k = 1 ⇒ умножаем все на 10^k = 10¹ = 10;

10X = 10 · 0,30555 ... = 3,05555 ...
10X − X = 3,0555 ... − 0,305555 ... = 2,75 = 11/4;
9X = 11/4;
X = (11/4) : 9 = 11/36.

Наконец, последняя дробь: X = 0,(2475) = 0,2475 2475 ... Опять же, для удобства периодические части отделены друг от друга пробелами. Имеем:

k = 4 ⇒ 10^k = 10⁴ = 10 000;
10 000X = 10 000 · 0,2475 2475 = 2475,2475 ...
10 000X − X = 2475,2475 ... − 0,2475 2475 ... = 2475;
9999X = 2475;
X = 2475 : 9999 = 25/101.

Смотрите также: