Простейшие показательные уравнения

5 февраля 2012

Если взять обычную степень и «засунуть» в показатель переменную x , получим показательное уравнение. Таких уравнений великое множество, и для них есть собственные методы решения.

Сегодня мы познакомимся с простейшими конструкциями. Они так и называются — простейшие показательные уравнения (кэп?). Все остальные, как бы сложно они ни выглядели, в итоге сводятся к простейшим. Но это уже материал следующих уроков.

Простейшее показательное уравнение — это уравнение вида:

a ^x = b , где a > 0, a ≠ 1

Такое уравнение не имеет корней при b ≤ 0, а при b > 0 имеет единственный корень: x = log _a b . Более сложные показательные уравнения решаются по следующей схеме:

Перевести все степени к одинаковому основанию. Желательно, чтобы оно было целым и минимальным. Например, вместо 4^x лучше писать 2^2
x, а вместо 0,01^x — вообще 10^−2
x. Почему — узнаете из примеров;
В уравнениях, где есть умножение или деление, надо выполнить эти действия. Напомню: при умножении степеней с одинаковым основанием показатели складываются, при делении — вычитаются;
Если все сделано правильно, получим уравнение вида a ^{f
(
x
)} = a ^g
(
x
), где a — просто число. Его можно отбросить, поскольку показательная функция монотонна. Получим уравнение f ( x ) = g ( x ), которое легко решается.

Помните, что корни — тоже степени, но с дробным основанием:

Задача. Решите уравнение:

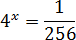
Итак, приведем все степени к основанию 2:

4^x = (2²)^x = 2^2
x; 1 = 2⁰; 256 = 2⁸

Теперь перепишем исходное уравнение и выполним деление:

Получили простейшее показательное уравнение. Отбрасываем основание — получаем:

2 x = −8 ⇒ x = −4

Задача. Решите уравнение:

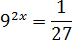
Снова приводим все степени к наименьшему целому основанию:

9^2
x = (3²)^2
x = 3^4
x; 1 = 3⁰; 27 = 3³

Обратите внимание: число 27 не является целой степенью девятки. Именно поэтому надо приводить все степени к основанию 3, а не 9. Возвращаемся к исходному уравнению:

Осталось избавиться от основания степени:

4 x = −3 ⇒ x = −3/4 = −0,75

Задача. Решите уравнение:

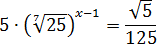
В уравнении присутствуют сразу 4 множителя, которые надо перевести в степени с одинаковым основанием:

Учитывая эти факты, перепишем исходное уравнение:

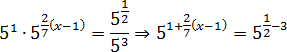
Избавимся от основания — и после приведения дробей к общему знаменателю получим классическую пропорцию:

Дальше все стандартно: произведение крайних элементов пропорции равно произведению средних. Имеем:

14 + 4 x − 4 = −35 ⇒ 4 x = −45 ⇒ x = −45 : 4 = −11,25

Ниже даны 12 тренировочных задач. Если что-то не получается — ничего страшного, потому что есть второй вариант этого теста (см. «Простейшие показательные уравнения — 2 вариант»). Попробуйте решить его.

Смотрите также: