Перед любыми манипуляциями с корнями полезно вспомнить свойства степеней с натуральным показателем. Я группирую эти свойства в три блока.
1. Умножаем и делим степени с одинаковым основанием — меняется только показатель:
\[\begin{align} & {{a}^{x}}\cdot {{a}^{y}}={{a}^{x+y}} \\ & \frac{{{a}^{x}}}{{{a}^{y}}}={{a}^{x-y}} \\ & {{\left( {{a}^{x}} \right)}^{y}}={{a}^{x\cdot y}} \\ \end{align}\]
2. Умножаем и делим степени с одинаковым показателем — меняется основание:
\[\begin{align} & {{\left( a\cdot b \right)}^{x}}={{a}^{x}}\cdot {{b}^{x}} \\ & {{\left( \frac{a}{b} \right)}^{x}}=\frac{{{a}^{x}}}{{{b}^{x}}} \\ \end{align}\]
3. Чётные степени «сжигают» минусы, нечётные — нет:
\[\begin{align} & {{\left( -a \right)}^{2n}}={{a}^{2n}} \\ & {{\left( -a \right)}^{2n+1}}=-\left( {{a}^{2n+1}} \right) \\ \end{align}\]
Мы будем использовать эти свойства на всю катушку в третьей части урока. А пока начнём с более простых вещей.
При работе с корнями многие ученики допускают одну и ту же ошибку. Они пытаются подменить чёткие правила алгебры интуитивными размышлениями. И на первый взгляд всё выглядит хорошо. Взгляните на примеры:
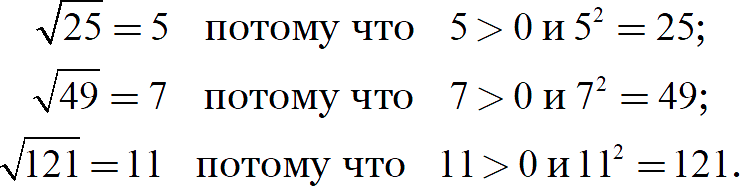
Во всех трёх случаях мы видим, что под корнем стоят точные квадраты. Их можно переписать так:
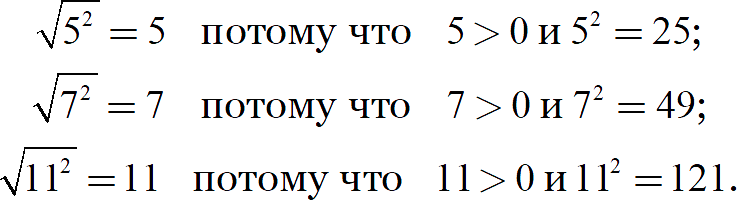
Может показаться, что для упрощения выражения достаточно убрать степень и знак корня. На практике это не так:
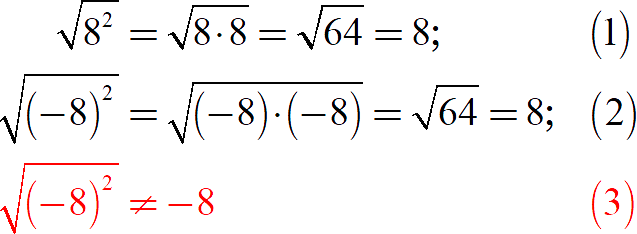
Из третьей строки видно, что просто убрать степень и корень с отрицательного основания нельзя, ведь корень не может быть отрицательным! Вторая строка объясняет нам, что именно происходит: квадрат делает число под корнем положительным, а дальше мы извлекаем этот самый корень и вновь получаем положительное число. В итоге строки 1 и 2 ведут к извлечению корня из одного и того же числа — 64.
Вывод?
А вывод такой: корень из квадрата не меняет положительные числа, а отрицательные меняет на противоположные. Это в точности совпадает с определением модуля:
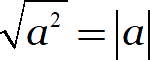
Для удобства дальнейших размышлений предлагаю взять на вооружение вот такое определение модуля:
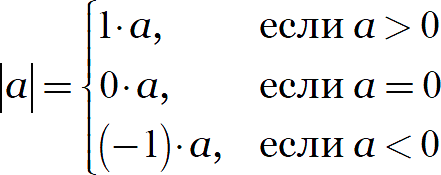
Это определение чрезвычайно полезно для решения сложных задач с параметрами. Об этом как-нибудь в следующий раз. А пока давайте потренируемся:
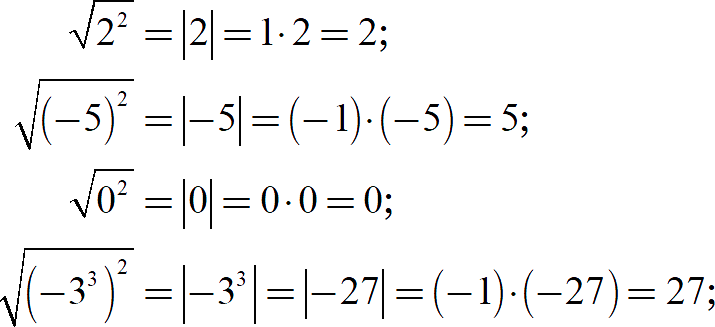
Опыт моих учеников: поначалу довольно непривычно выписывать эти множители (1, 0 и −1), но затем человек привыкает и пишет всё на автомате. А затем и вовсе перестаёт писать — всё происходит в его голове, но навык добавления множителей остаётся (и очень пригодится, когда мы считаем коэффициенты многочленов).
Потренируйтесь самостоятельно:
Задание. Найдите значение выражения:
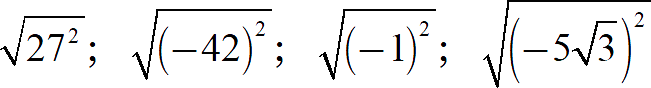
[Показать ответы]
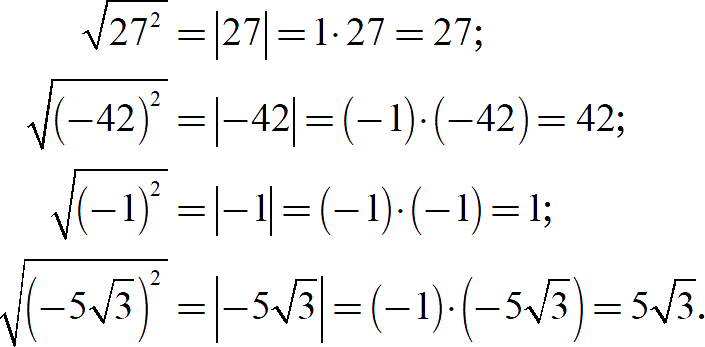
Отдельное внимания заслуживают двойные корни, вложенные друг в друга:
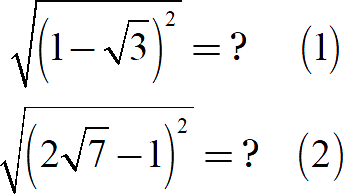
Для них замена корня модулем тоже работает, но возникает вопрос: как корректно раскрыть модуль? Придётся сравнивать корни:
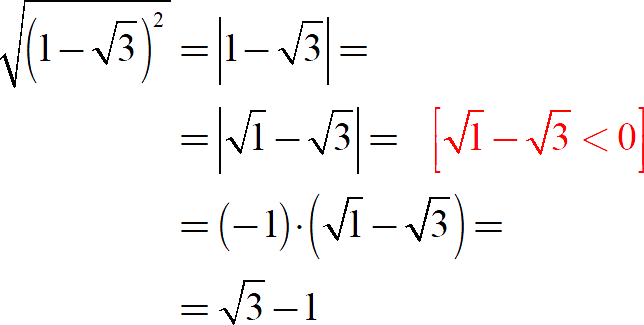
Откуда такое смелое утверждение во второй строке? Существует два способа доказать неравенство в красных скобках:
Я приведу оба:
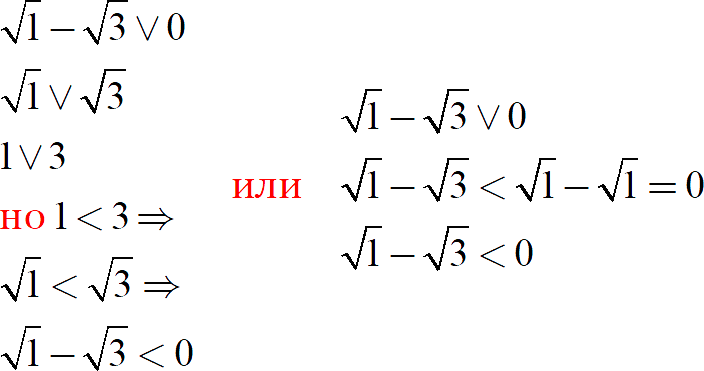
Сравнение корней — отдельная серьёзная тема. Ей посвящён целый урок. Поэтому давайте просто решим второе задание:
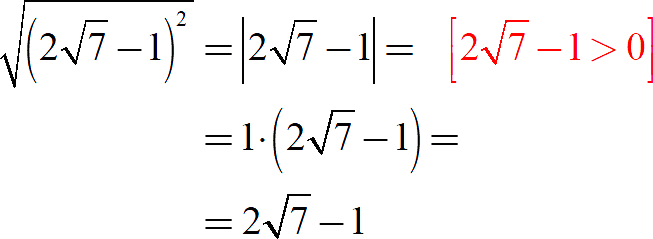
Задание. Вычислите значение выражения:
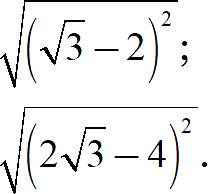
[показать ответ]
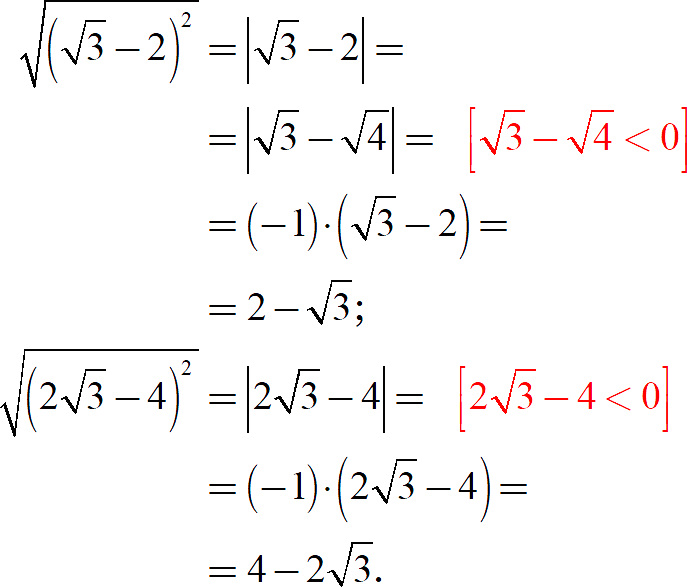
Идём дальше. Вновь запишем нашу волшебную формулу:
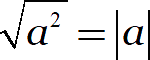
Капитан очевидность как бы намекает: эта формула верна не только для квадратов, но и для всех чётных степеней:
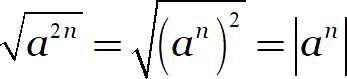
Другими словами, корень из любой чётной степени понижает эту степень ровно в два раза, но взамен навешивает на неё модуль! Рассмотрим примеры:
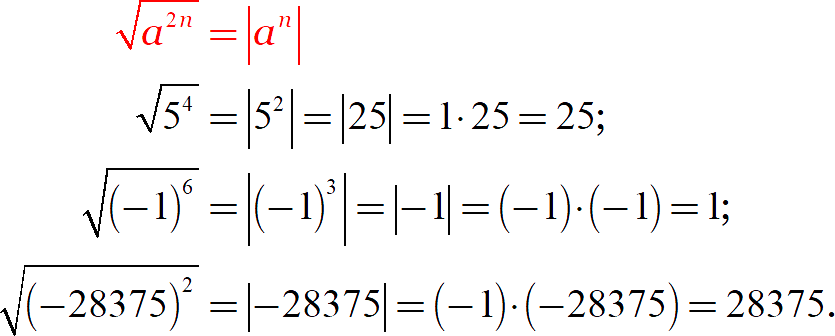
Обратите внимание на последнюю строку: изначально под корнем стоит довольно громоздкое число. Вычислять его напролом — возводить в квадрат, а затем извлекать корень — безумие. Но формула понижения степени редуцирует задачу до устной — отличная экономия времени на экзамене.:)
Попробуйте сами:
Задание 2. Найдите значение выражения:
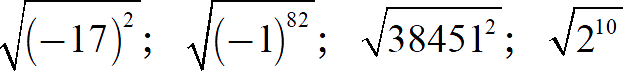
[Показать ответы]
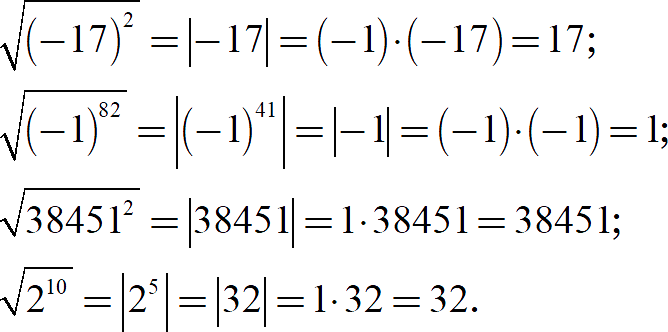
Вывод: если видите корень из степени, то смело понижайте степень вдвое, убирайте корень, но взамен ставьте модуль. Всегда. Обязательно. Ок? Переходим ко второй части урока.
Перед тем как давать какие-либо новый формулы, напомню важный факт. Корень из суммы не равен сумме корней:
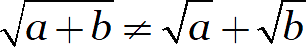
Иначе мы бы получили вот такие бредовые выкладки:
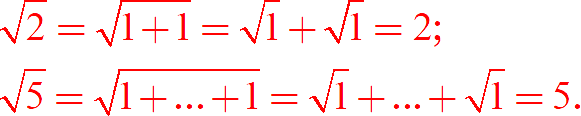
Вроде бы, капитаноочевидно, но многие даже в старших классах допускают такие ошибки.
А теперь разберём ещё два свойства корней.
Корни можно умножать и делить. Правила просты:
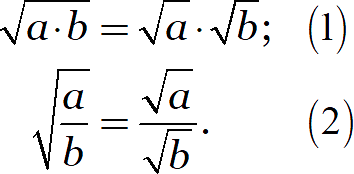
Примеры:
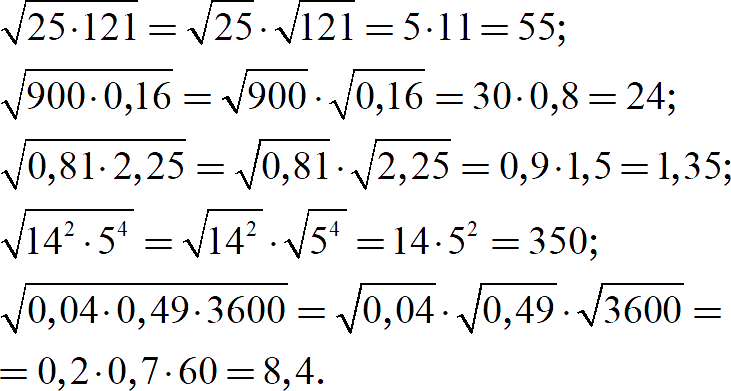
Попробуйте сами:
Задание 3. Найдите значение выражения:
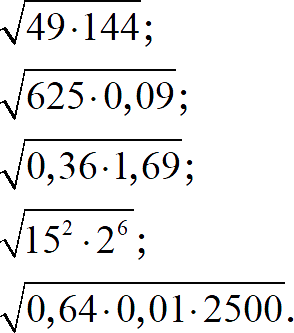
[показать ответы]
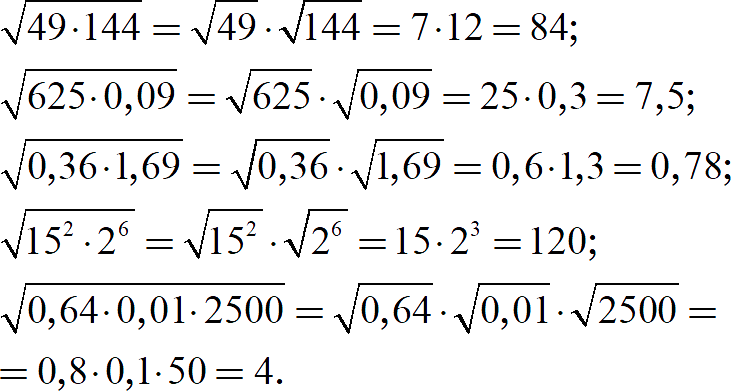
Как видите, с помощью формул мы разбиваем сложный корень на несколько простых.
Мы знаем, то все формулы работают как слева-направо, так и справа-налево, поэтому корни можно «склеивать». При этом новый корень может легко вычисляться, хотя исходные части — не вычисляются вообще. Например:
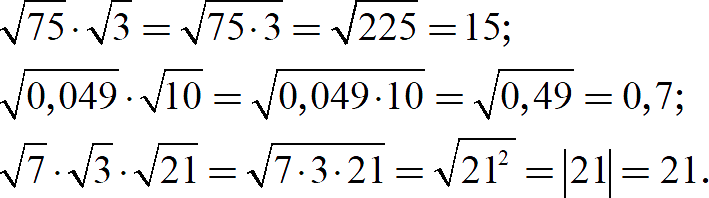
Попробуйте повторить этот трюк:
Задание 4. Найдите значение выражения:
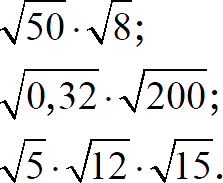
[показать ответы]
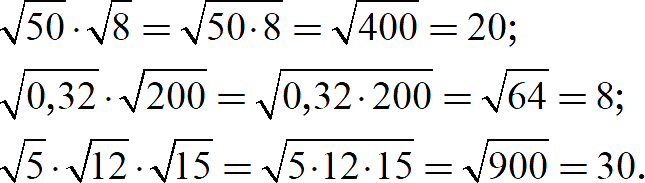
Но есть одна тонкость. Взгляните, например, на формулу произведения корней:

Напомню: знак радикала обозначает арифметический квадратный корень, который извлекается только из неотрицательных чисел и сам является числом неотрицательным.
С левой стороны от знака равенства стоит один корень, а справа — целых два. Поэтому области определения левой и правой части этого равенства различны:
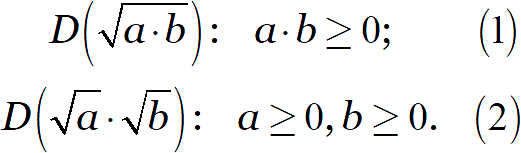
В чём конкретно состоит различие?
В первой строке мы видим произведение, поэтому неравенство (1) верно всякий раз, когда знаки множителей совпадают. В частности, оба множителя могут быть отрицательными, но их произведение всё равно будет положительным.
Вторая строка — система из двух неравенств, и здесь отрицательные числа нас уже не устроят. Вывод:
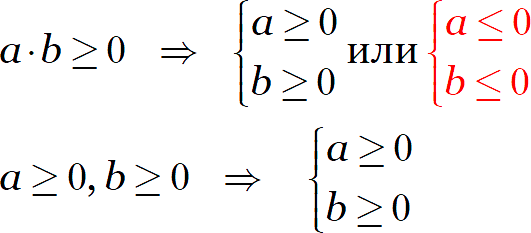
Красным я выделил ситуацию, которая допустима для корня из произведения, но становится недопустимой для произведения корней.
Поскольку любое равенство определено лишь тогда, когда определена и левая, и правая его части, дополним исходные правила специальными требованиями:
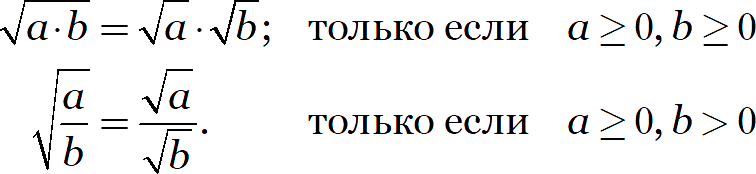
И вот в таком виде их уже можно использовать — везде и всегда!
Может показаться, что эти ограничения несущественны. Или искусственны. Чуть выше мы никак их не учитывали и всё прекрасно посчитали. Поэтому вопрос: когда ограничения области определения становятся существенным?
Ответ: когда под корнями стоят не конкретные числа, а переменные. К примеру, пусть даны числа:
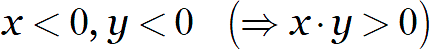
Очевидно, что произведение двух отрицательных чисел будет положительным. И хотя корень из произведения будет определён, извлекать корни из отдельных множителей нельзя:
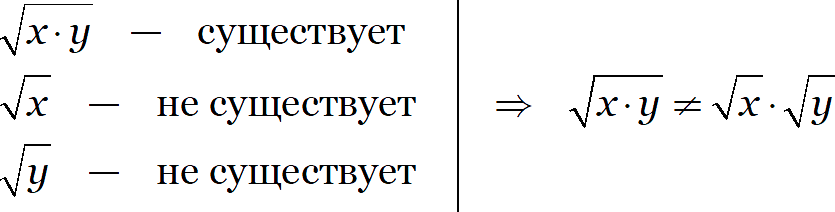
Значит, нужно сделать так, чтобы множители под корнем стали положительными. И тут нам на помощь приходит старое доброе число −1:
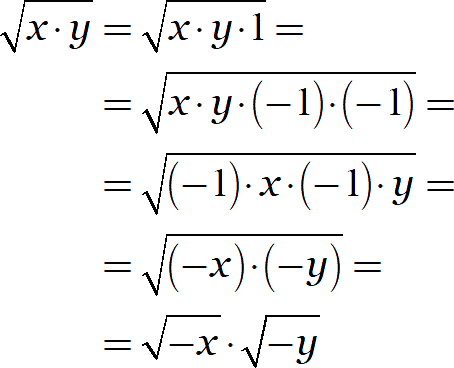
Добавление минусов к каждому из двух множителей нисколько не повлияло на произведение, но привело к возникновению двух новых множителей, каждый из которых уже точно положителен:
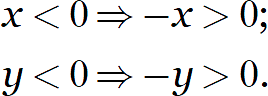
Помните об этом преобразовании, когда сталкиваетесь с произведением отрицательных выражений под знаком корня. Источником такой отрицательности могут быть условия задачи, либо следствия из области определения (такое часто встречается в логарифмических уравнениях и неравенствах, которые изучаются в 10—11 классах).
Ну а мы немного потренируемся и пойдём к третьей части урока — работе с переменными.
Задание 5. Найдите значение выражения:
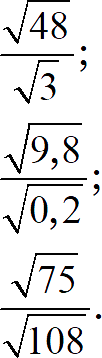
[показать ответы]
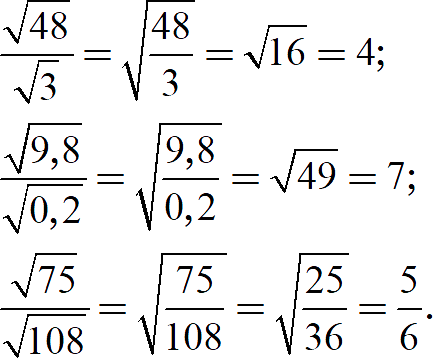
Переходим к самому весёлому.:)
Если не считать определения, то мы знаем о корнях две вещи. Во-первых, корни понижают степени, но добавляют модули:
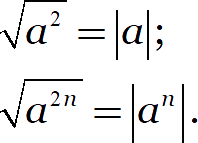
Во-вторых, корни можно умножать и делить. Но не всегда:
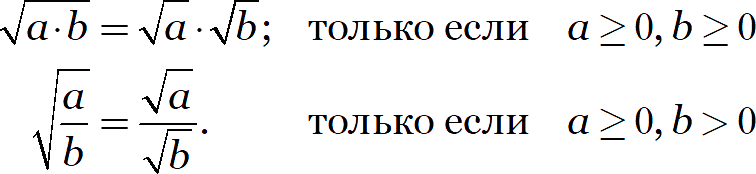
До сих пор мы тренировались лишь на конкретных числах. И многие могут удивляться: зачем все эти рассуждения про модули и ограничения?
Сейчас мы заменим числа буквами — и задача резко усложнится. Или не усложнится — если вы внимательно изучите то, что написано дальше.:)
Начнём с простого. Мы уже знаем, как избавляться от точной степени:
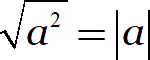
Попробуем применить эту формулу к двум различным выражениям:
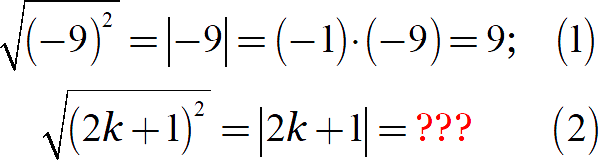
В первой строке мы без труда раскрыли модуль, поскольку знаем, что число под модулем отрицательно. Затем посчитали — получили ответ.
Но как раскрыть модуль во второй строке? Ведь правила раскрытия будут меняться в зависимости от того, какое значение принимает переменная. И если никаких дополнительных ограничений на переменную нет, то модуль так и останется нераскрытым. Взгляните:
Замените выражение тождественно равным, не содержащим знака корня:
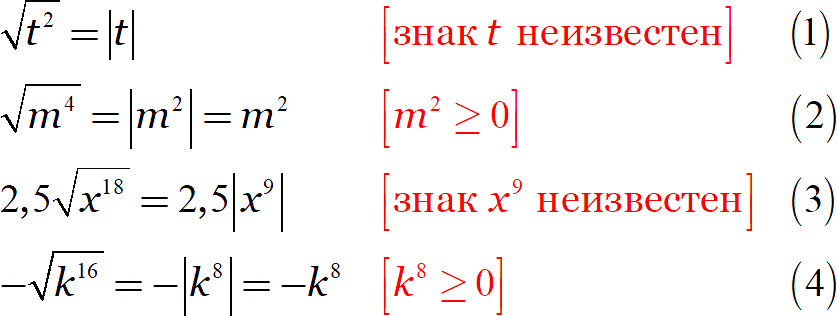
Из приведённых примеров видно:
Почему? Чётные степени в строках (2) и (4) при любом значении переменной будут положительным числом или нулём. Поэтому модуль однозначно раскрывается со знаком «плюс».
Нечётная степень в строках (1) и (3) таким свойством не обладает: она может оказаться как положительным числом, так и отрицательным. Поэтому модуль раскрыть нельзя.
Попробуйте сами:
Задание. Замените выражение тождественно равным, не содержащим знака корня:
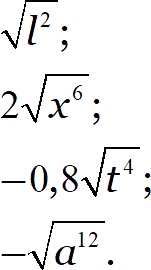
[показать ответ]
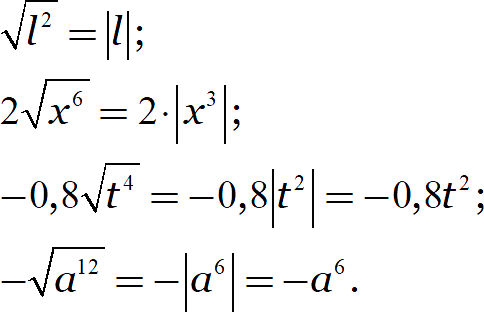
Чётные степени всегда неотрицательны, нечётные степени могут принимать любой знак:
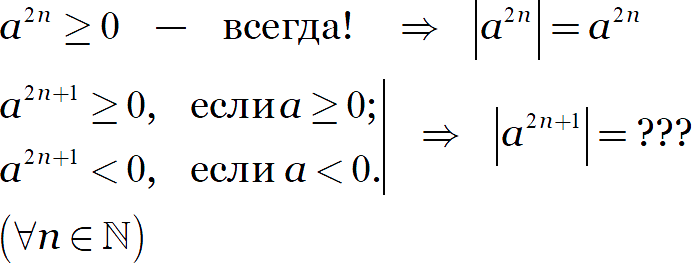
Тем не менее, модуль нечётной степени тоже можно раскрыть. Если в задаче есть дополнительные условия.
Зачастую в самом условии задачи содержатся ограничения на переменную, которые помогают однозначно раскрыть модуль. Пример:
Упростите выражение:
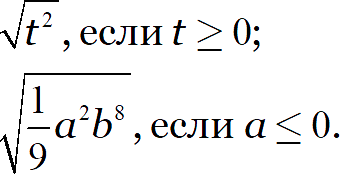
Работаем по тем правилам, которые изучали выше:
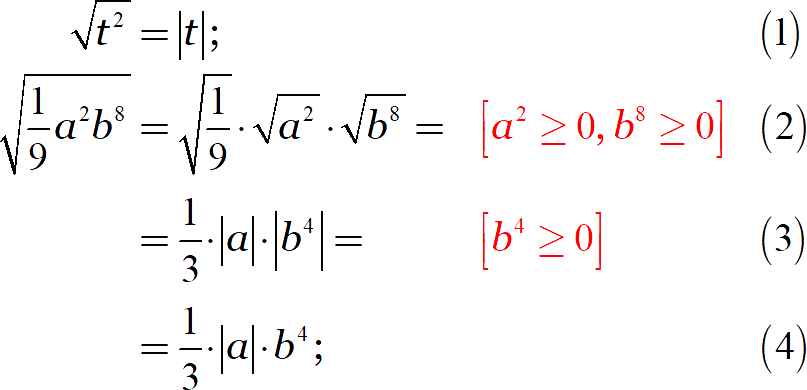
Обратите внимание: в строке (2) чётные степени под корнем дают три неотрицательных числа, поэтому корень можно разбить на три изолированных множителя — область определения при этом не поменяется; затем в строке (3) мы видим чётную степень под модулем и раскрываем его.
Ещё раз запишем результат и дополним его исходными условиями:
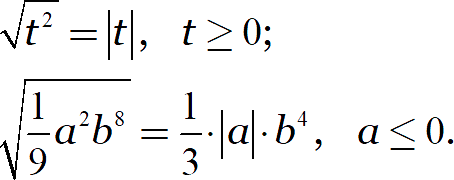
В первом случае выражение под модулем положительно или ноль, поэтому модуль однозначно раскрывается со знаком «плюс». Во втором — отрицательно или ноль, поэтому модуль раскрывается со знаком «минус»:
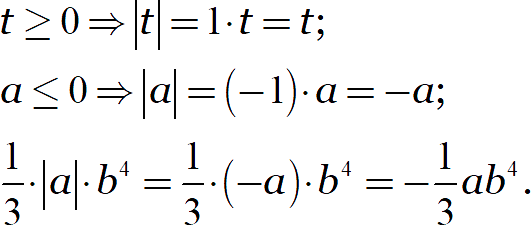
Возможно, у вас возникает вопрос: почему мы пишем множитель 1 или −1, но не рассматриваем отдельно множитель 0? В этом фишка модуля:
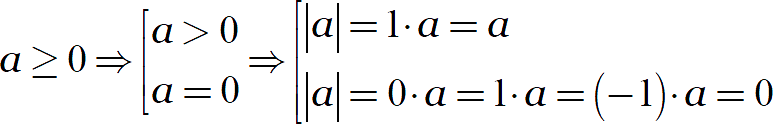
Таким образом, в нуле модуль можно раскрывать любым удобным способом.
Попробуйте самостоятельно:
Задание. Упростите выражение:
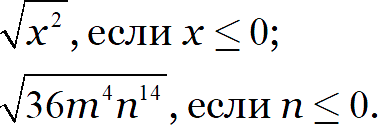
[показать ответ]
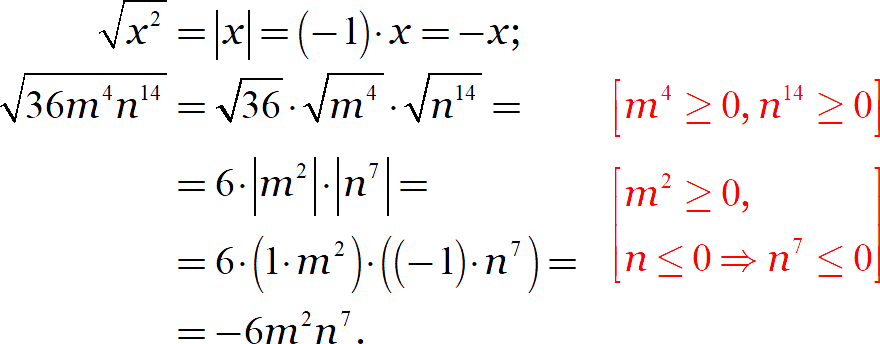
Это были весьма примитивные выражения, сводящиеся к раскрытию модуля. На них мы отработали важный новый навык. Теперь воспользуемся этим навыком для решения более интересных задач.
Последний и самый интересный раздел этого урока.
Откуда берутся дополнительные ограничения на переменные? Существует ровно два источника таких ограничений:
Начнём с первого пункта — ограничений, явно указанных в условии задачи. Примеры:
Упростите выражение:

С первым выражением всё просто:
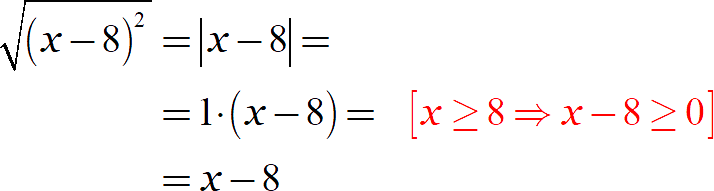
Со вторым уже интереснее. Заметим, что в первом числителе стоит формула сокращённого умножения, а дробь под корнем гарантированно имеет неотрицательный числитель и знаменатель:
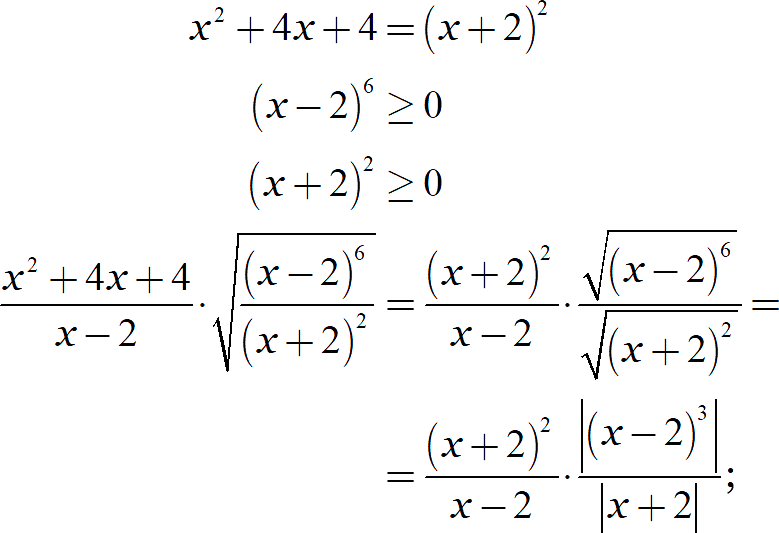
Вспомним исходные ограничения:
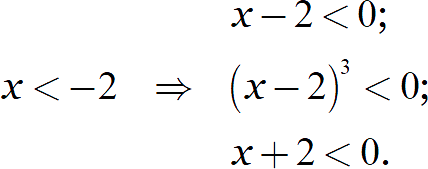
И раскроем модули:
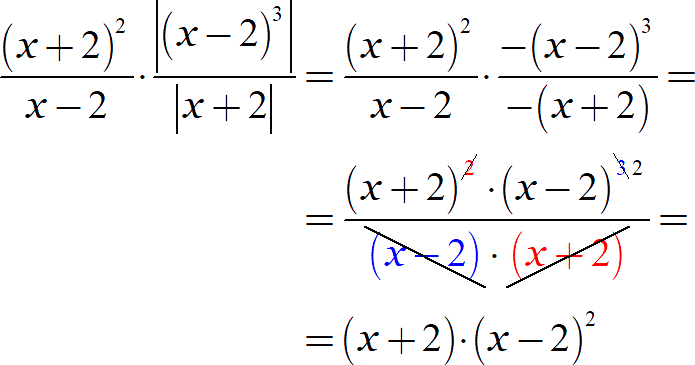
Как видите, нам удалось избавиться не только от модулей, но и от дробей.:)
Обратите внимание
Материал, представленный дальше, относится скорее к следующему уроку — «Внесение и вынесение множителей из-под знака корня». Его изучение прямо сейчас не является обязательным, но может оказаться весьма полезным для сильных учеников.
Наконец, разберёмся с неявными ограничениями. Ещё раз запишем самую первую формулу:
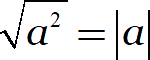
Пусть известно, что подмодульное выражение неотрицательно. Тогда модуль можно убрать:
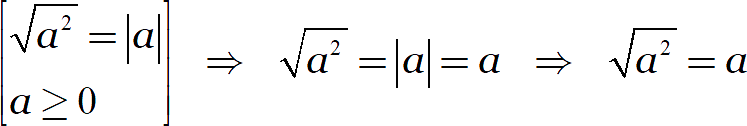
С отрицательными величинами тоже можно провернуть такой трюк:
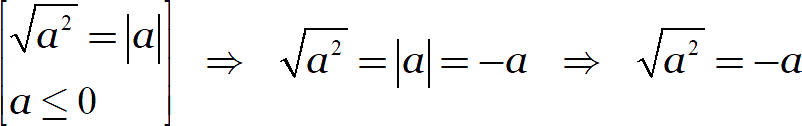
Но любое равенство работает как слева-направо, так и справа-налево. Следовательно, если нам известен знак переменной, мы можем внести её под знак корня:
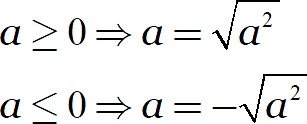
Это замечание позволит упрощать выражения, которые неподготовленному ученику покажутся неприступными.
Остаётся лишь один вопрос: где взять знак переменной? Ответ: ограничения на переменную часто скрыты в области определения. Например:
Упростите выражения:
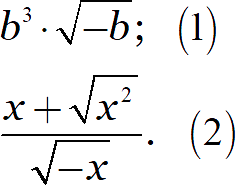
Решение:
В первой строке мы видим корень, поэтому выпишем область определения. Это даст нам ограничения на переменную и поможет внести её под знак корня:
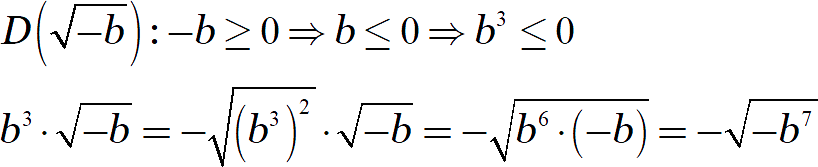
То же самое со вторым выражением:
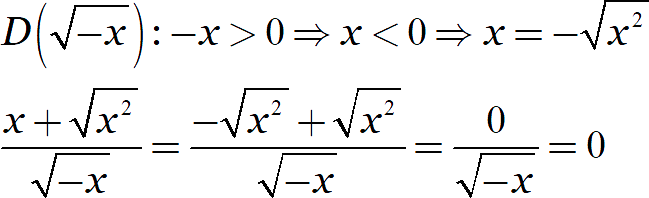
В итоге мы получили выражение, тождественно равное нулю. Однако помните: это равенство сохраняется только для отрицательных значений переменной! Для положительных значений исходное выражение вообще не определено.
Операция, которую мы только что провернули, как раз и называется внесением переменной под знак радикала.
В заключение хотел бы рассмотреть типичную ситуацию для сложных алгебраических задач, когда под корнем стоят, на первый взгляд, противоположные числа.
Упростите выражение:
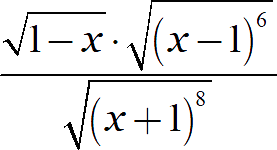
Заметим, что самый первый корень накладывает жёсткие ограничения на переменную:
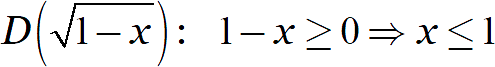
Под остальными корнями стоят неотрицательные выражения, поэтому дальше всё просто:
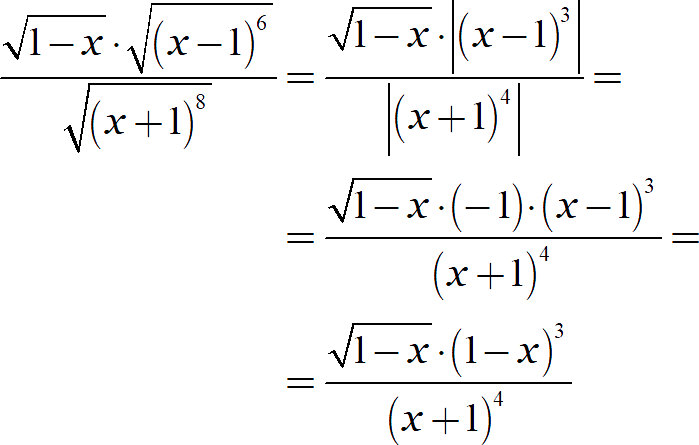
Наличие неявного ограничения позволило нам раскрыть модуль даже у нечётной степени. Обратите внимание на этот переход:
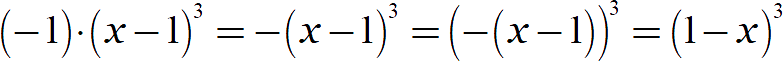
Как мы помним из краткой вводной, минусы можно выносить (и вносить) из основания нечётной степени. Это можно сделать как после раскрытия модуля, так и в самом начале — прямо под корнем:
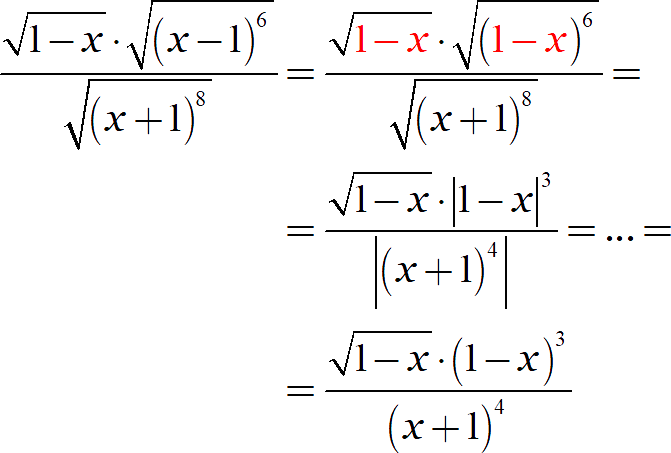
Красным я отметил одинаковые выражения, стоящие под корнем и в основании степени. Именно такая форма записи (а не игра с минусами) является предпочтительной, например, в логарифмических уравнениях и неравенствах.
Но это тема совсем другого урока. А на сегодня хватит.:)